Question

Докажите, что хорды окружности, находящиеся на одном и том же расстоянии от её центра, равны между собой
Верно ли обратное утверждение?

Answer 1

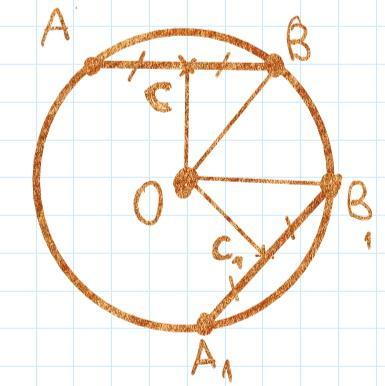
Рассмотрим произвольную хорду, проведем к ней перпендикуляр. По известному свойству основание перпендикуляра будет совпадать с серединой хорды, то есть AC = CB (см. рисунок), отрезок OB - радиус окружности. ΔOCB - прямоугольный (∠С = 90°)

Рассмотрев другую хорду (A₁B₁) и соответствующий ΔOC₁B₁, получаем:

1) OC = OC₁ (по условию) ⇒ ΔOCB = ΔOC₁B₁ ( по катету и гипотенузе) ⇒ CB = C₁B₁ ⇒ AB = A₁B₁, то есть удаленные на равные расстояния от центра хорды равны.

2) AB = A₁B₁ (по условию) ⇒ ΔOCB = ΔOC₁B₁ ( по катету и гипотенузе) ⇒ OC = OC₁, то есть обратное утверждение также верно.