Предмет: Алгебра,
автор: gyyftghutfjy
Помогите пожалуйста
289.Найдите сумму целых решений неравенств
Приложения:
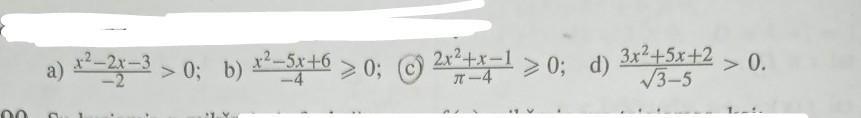
Ответы
Автор ответа:
1
Ответ:
Объяснение:
а)
x∈∅
x∈ ( -1; 3 )
b)
x∈∅
x∈ [ 2; 3 ]
с)
x∈∅
x∈ [ -1; ]
d)
x∈∅
x∈ ( -1 ; - )
gyyftghutfjy:
благодарю!!!
Похожие вопросы
Предмет: Русский язык,
автор: mihaylovada
Предмет: Русский язык,
автор: adilgulbala
Предмет: Английский язык,
автор: Диана12353
Предмет: Геометрия,
автор: дмитрий462
Предмет: Биология,
автор: anahitpapoyan2