Предмет: Геометрия,
автор: olesechka2004
Основания равнобедренной трапеции равны 27 и 63, боковая сторона равна 30. Найдите длину диагонали трапеции.
Ответы
Автор ответа:
12
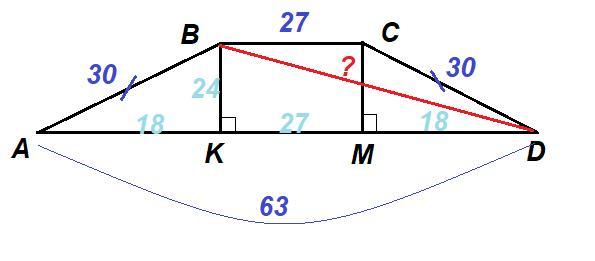
Дано: ABCD - трапеция; AD║BC;
AB=CD=30; BC = 27; AD = 63.
Найти: BD - ?
Решение:
У равнобедренной трапеции диагонали равны:
BD = AC.
Построим две высоты BK и CM. Полученная фигура KBCM - прямоугольник, у которого противоположные стороны равны:
BC = KM = 27.
ΔABK = ΔDCM по равным гипотенузам (AB=CD)
и равным катетам (BK= CM).
Тогда
AK = MD = (AD - KM) : 2 = (63 - 27) : 2 = 18
ΔAKB - прямоугольный, по теореме Пифагора:
ΔDKB - прямоугольный, по теореме Пифагора:
Ответ: диагональ трапеции равна 51.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: sveta19871
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: 79872617224
Предмет: Математика,
автор: Виктория22557
Предмет: Химия,
автор: tugasmanov1