Предмет: Математика,
автор: whiteen
Помогите решить уравнение, расписать, но не сложным действием (это логарифмическое уравнение)
Приложения:
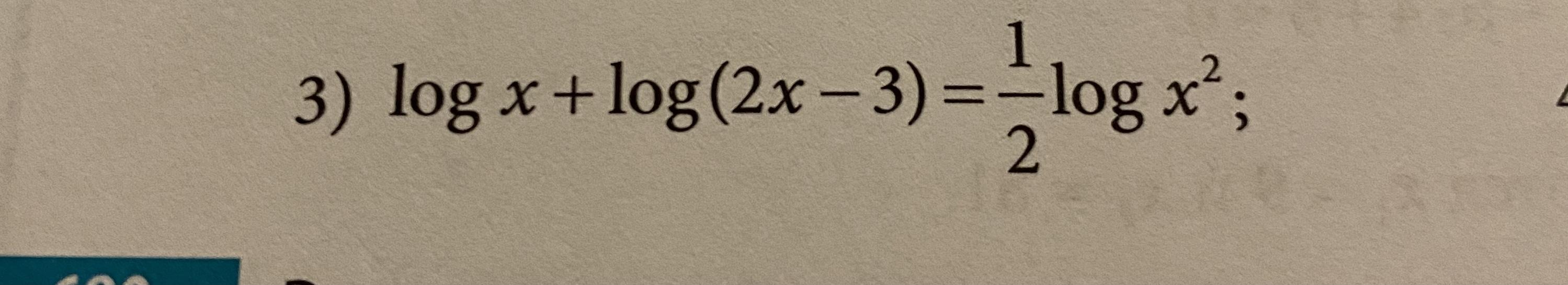
Ответы
Автор ответа:
0
Ответ:
По свойству логарифмов log(a)+log(b)=log(ab) преобразуем левую часть уравнения
По свойству логарифмов преобразуем правую часть уравнения
Так как основания логарифмов равны , можем приравнять их аргументы
Похожие вопросы
Предмет: Русский язык,
автор: olyaolyaolya36
Предмет: Русский язык,
автор: Polinka37
Предмет: Русский язык,
автор: aknieto007
Предмет: Алгебра,
автор: tanyaalpatova142
Предмет: Алгебра,
автор: FARALAV