Предмет: Алгебра,
автор: MQly
Исследовать на чётность функции
Приложения:
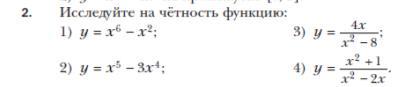
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: sakengibrat
Предмет: Русский язык,
автор: katrinkostuk
Предмет: Русский язык,
автор: neznakomkanet
Предмет: Литература,
автор: edinstvennaya1
Предмет: Обществознание,
автор: dimas146