Предмет: Математика,
автор: ptimofej397
Помогите пожалуйста прошу
Приложения:

Ответы
Автор ответа:
1
Ответ:
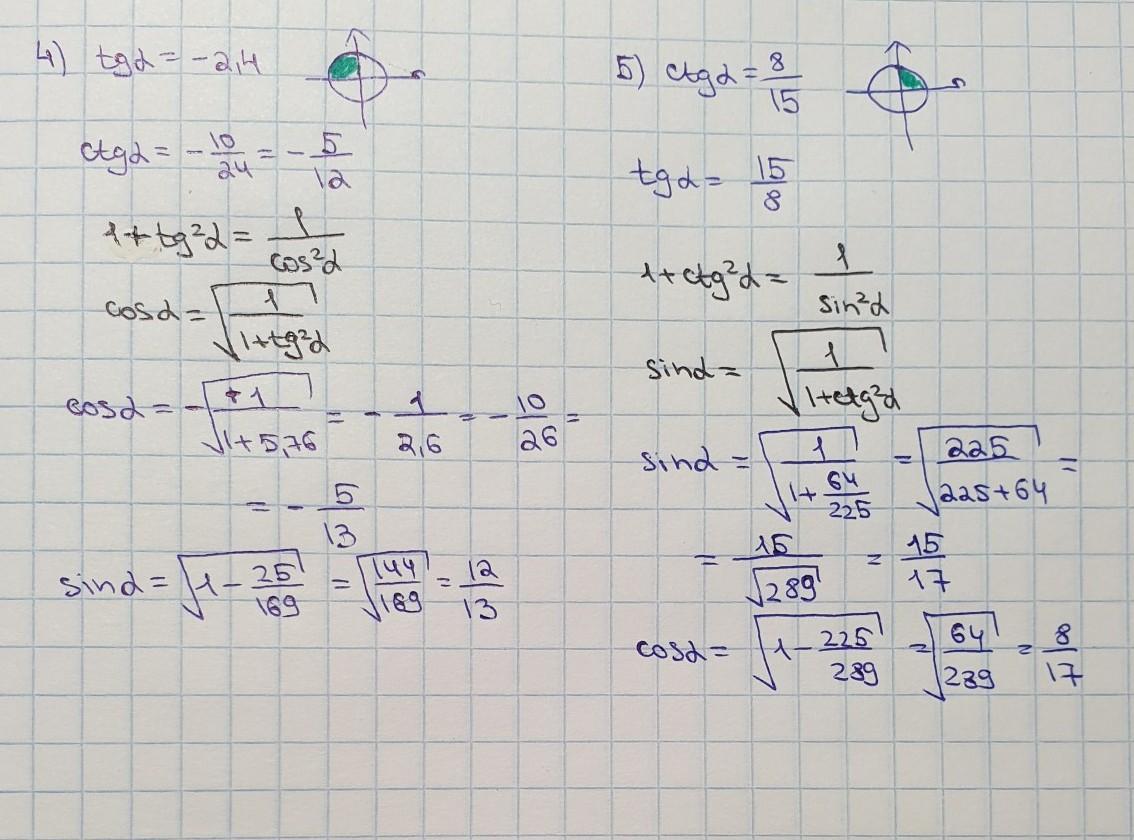
решение на фотографиях
Приложения:

ptimofej397:
спасибо большое
помогите ещё раз пожалуйста, задание в профиле
Автор ответа:
1
Ответ:
В зависимости от угла α определяем знак и применим следующие формулы:
Так как в этой четверти cosα<0, то
Так как в этой четверти sinα>0, то
Так как в этой четверти cosα<0, то
Так как в этой четверти sinα>0 и cosα<0, то
Так как в этой четверти sinα>0 и cosα>0, то
здравствуйте помогите пожалуйста прошу вас, задание в профиле, математика
Похожие вопросы
Предмет: Русский язык,
автор: waystegsasha
Предмет: Русский язык,
автор: jasmin201426
Предмет: Русский язык,
автор: sadx
Предмет: Математика,
автор: Александракул
Предмет: Математика,
автор: mashenkaguzano