Предмет: Математика,
автор: Dareit
Решение показательных уравнений
написать в тетради
Приложения:
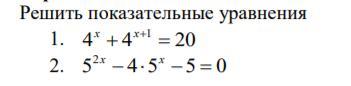
Ответы
Автор ответа:
1
Ответ:
1). х=1
2).х=1
Пошаговое объяснение:
1).
х=1
2)
- показательное квадратное уравнение, замена переменной:
t1=-1 - посторонний корень
обратная замена:
х=1
Похожие вопросы
Предмет: Математика,
автор: stenat80
Предмет: Русский язык,
автор: Polina220903
Предмет: Другие предметы,
автор: liza12943
Предмет: Химия,
автор: artemmamaggg
Предмет: Биология,
автор: kosmos71