нужно найти пример трапеции

Ответы
2) Из вершины D продлим сторону до пересечения на продлении стороны BC, так что AB ║ DE, т.е. ABED — параллелограмм.
∠A = ∠E = 60° (противоположные углы у параллелограмма равны)
Так как AB = CD ⇒ ED = CD ⇒ ∠ECD = ∠CED = ∠CDE = 60°, т.е. треугольник CDE — равносторонний ⇒ CD = CE = ED = 32
Тогда AD = BC + CE = 20 + 32 = 52
P = 20 + 32 + 32 + 52 = 136
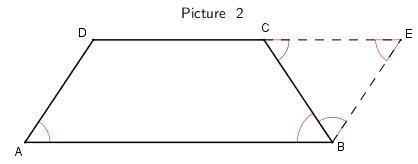
Рисунок 2.
Аналогично решению из рисунка 1, достроим до параллелограмма ADEB, AD ║ EB, мы имеем что ΔCEB - равносторонний, т.е. CE = CB = EB = 20, тогда CD = AB - CE = 32 - 20 = 12.
P = 12 + 20 + 20 + 32 = 84
3)
Дано: равнобедренная трапеция АВСD.
АВ=СD.
Меньшее основание ВС=15 см. Большее основание AD=49 см. Острые углы D=A=60° (трапеция равнобедренная).
Найти: периметр трапеции Р=?
Решение:
Опустим перпендикуляры к большему основанию СN и ВM. МN=BC=15 cм, АМ=АN=(49-15):2=17 см.
Рассмотрим треугольник АВМ. Угол А=60°, следовательно угол В=30°, т.к. сумма острых углов прямоугольного треугольника=90°.
Катет лежащий против угла в 30° равен половине гипотенузы, значит АВ = 2·АМ = 2*17=34 см.
Теперь известны все стороны трапеции АВ=СD=34см, ВС=15см, АD=49см.
Р=34*2+15+49=132 см.
4) На фото.
7) На Фото
8)
DC║KB - как отрезки лежащие на основании трапеции.
DK║CB - по условию, поэтому DCBK - параллелограмм, значит DK=CB и ∠KBC=∠KDC=∠2; ∠AKD=∠KBC - как соответственные.
∠DAB=∠ABC - как углы при основании трапеции. В итоге в ΔADK все 3 угла равны, значит он равносторонний.
KB=DC=14,15 см как противоположные стороны параллелограмма.
AK=AB-KB=27,65см - 14,15 см=13,5 см. AD=AK=13,5 см - как стороны равностороннего треугольника. AD=BC - по условию.
P(ABCD) = AB+BC+CD+DA = 27,65см+13,5см+14,15см+13,5см = 41,8см+27см = 68,8см
8)