ВСЕМ СПАМЕРАМ БАН
Если нарисовать правильный треугольник со стороной n и разделить его на правильные треугольники со стороной 1, то получится n2 маленьких треугольников.
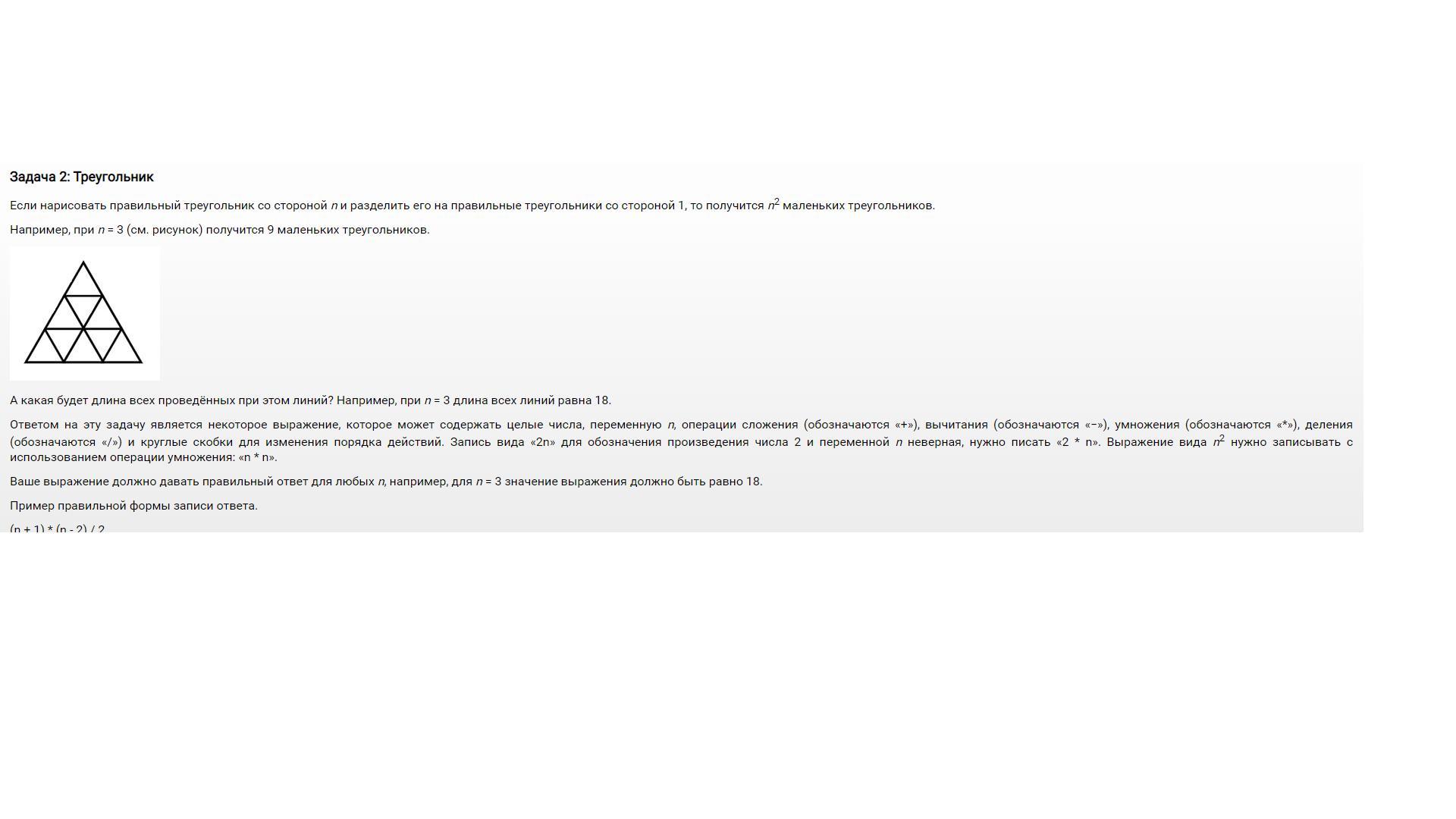
Например, при n = 3 (см. рисунок) получится 9 маленьких треугольников.
А какая будет длина всех проведённых при этом линий? Например, при n = 3 длина всех линий равна 18.
Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменную n, операции сложения (обозначаются «+»), вычитания (обозначаются «−»), умножения (обозначаются «*»), деления (обозначаются «/») и круглые скобки для изменения порядка действий. Запись вида «2n» для обозначения произведения числа 2 и переменной n неверная, нужно писать «2 * n». Выражение вида n2 нужно записывать с использованием операции умножения: «n * n».
Ваше выражение должно давать правильный ответ для любых n, например, для n = 3 значение выражения должно быть равно 18.
Пример правильной формы записи ответа.
(n + 1) * (n - 2) / 2
сколько треугольников будут свои стороны учитывать дважды
Ответы
Ответ:
n * 3 + (n * ( n - 1) / 2 * 3)
первая часть до плюса, это я обозначил стороны большого треугольника, в который входят все треугольники
а после плюса, я считал "внутренние стороны" в большом треугольнике
я нашел закономерность:
при построении мы можем нарисовать сначала один большой треугольник, а потом в нем строить маленькие,
а можем их выстраивать "кубиками", то есть сначала нижний ряд (количество N) так чтобы одна вершина у маленьких треугольников была выше других двух, а потом выстраиваем "перевернутые треугольнички", эти треугольники нам и помогут
чтобы их посчитать, у нас всегда будет такая закономерность:
(n - 1) + (n - 2) + (n - 3) +......+ 3 + 2 + 1 (при значениях n больше 10)
такую последовательность можно сократить вот таким вот образом:
(n * ( n - 1) / 2)
и получим правильное количество перевернутых треугольников
осталось только посчитать кол-во их сторон
( n - 1) / 2 * 3)
и сложить с первой частью
n * 3 + (n * ( n - 1) / 2 * 3)