Question

В правильной четырехугольной пирамиде SABCD все ребра равны 1. Найдите расстояние от вершины S до прямой
а) АВ ; б) АС

Answer 1

Ответ:

а) (√3)/2 ед.

б)  (√2)/2 ед.

Объяснение:

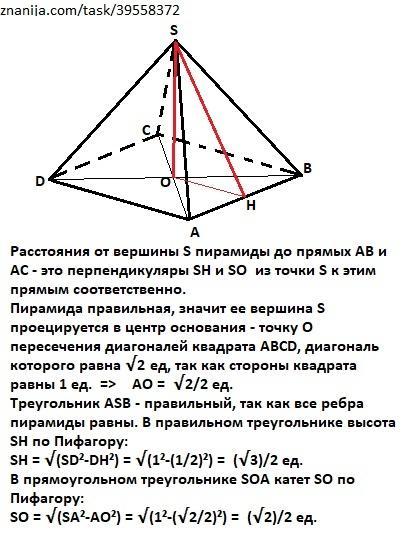
Расстояния от вершины S пирамиды до прямых АВ и АC - это перпендикуляры SH и SO  из точки S к этим прямым соответственно.  

Пирамида правильная, значит ее вершина S проецируется в центр основания - точку О пересечения диагоналей квадрата АВСD, диагональ которого равна √2 ед, так как стороны квадрата равны 1 ед.  =>  АО =  √2/2 ед.  (половина диагонали - свойство).

Треугольник ASB - правильный, так как все ребра пирамиды равны. В правильном треугольнике высота SH по Пифагору:

SH = √(SD²-DH²) = √(1²-(1/2)²) =  (√3)/2 ед.

В прямоугольном треугольнике SOА катет SO по Пифагору:

SО = √(SА²-АО²) = √(1²-(√2/2)²) =  (√2)/2 ед.