Решите квадратные неравенства!!!!!
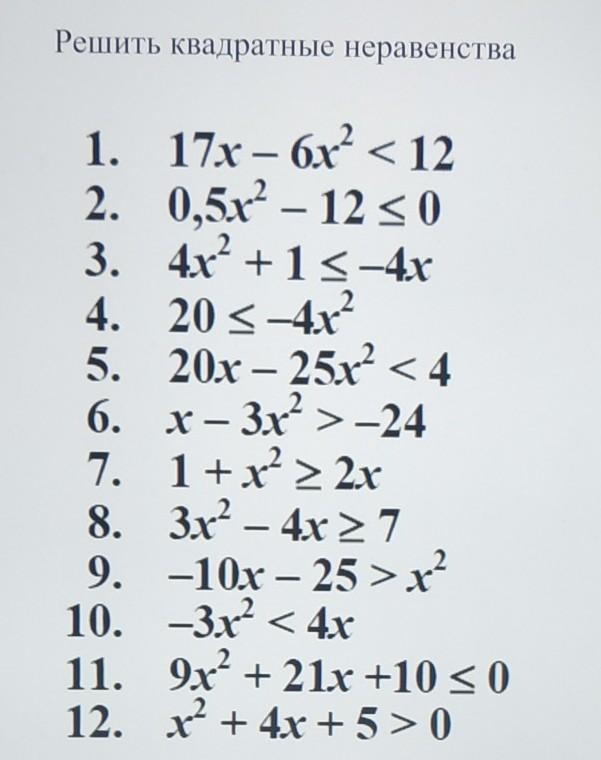
Ответы
Ответ:
Ответы после решения неравенства
Объяснение:
1) -6x^2+17x-12<0
-(2x-3)(3x-4)<0
x принадлежит (от - бесконечности до 4/3) и ( от 3/2 до + бесконечности)
2) 1/2 * x^2 <= 12
x^2 <= 24
2.1) x <= 2 * корень(6)
2.2) -x <= 2 * корень(6)
2.1) x принадлежит [от 0 до 2 корень(6)]
2.2) x принадлежит [от -2 корень(6) до 0), находим объединение:
x принадлежит [ от -2 корень(6) до 2 корень(6)]
3)4x^2+4x+1<=0
(2x+1)^2<=0
x = -1/2
4)4x^2 + 20<= 0
нет решений, тк левая часть всегда > 0
5)-25x^2+20x-4<0
(5x-2)^2>0
(5x-2)^2 = 0
x = 2/5
Любой x, кроме 2/5
6)-3x^2+x+24>0
(x-3)*(3x+8)<0
Методом интервалов:
x принадлежит (от -8/3 до 3)
7) x^2-2x+1>=0
(x-1)^2>=0
Любое значение x
8)3x^2-4x-7>=0
(x+1) * (3x-7)>=0
Методом интервалов:
x принадлежит (от -бесконечности до -1] и [от 7/3 до +бесконечности)
9)-x^2-10x-25>0
(x+5)^2<0
нет решений, тк левая часть всегда > 0
10)-3x^2-4x<0
x * (3x+4) > 0
Методом интервалов:
x принадлежит (от -бесконечности до -4/3) и (от 0 до +бесконечности)
11)9x^2+21x+10<=0
(3x+5)*(3x+2)<=0
Методом интервалов:
x принадлежит [от -5/3 до -2/3]
12) x^2 + 4x + 5 > 0
D < 0
Смотрим на левую часть, коэф a = 1 и a > 0, то левая часть > 0, следовательно может быть любое значение x