Предмет: Математика,
автор: KorInRus05
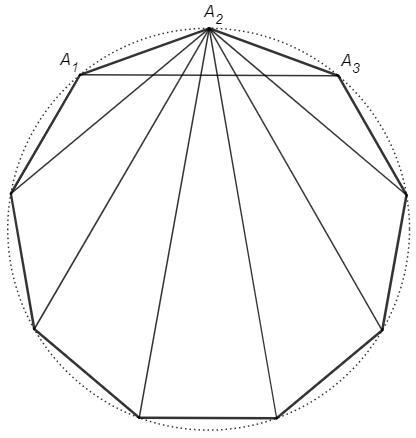
Назовём треугольник "хорошим", если одна из его сторон равна произведению двух других. Дан правильный многоугольник A1A2 . . . An со стороной 1. Диагонали, проведённые из A2, делят треугольник A1A2A3 на n − 2 треугольника. Докажите, что все они "хорошие".
Ответы
Автор ответа:
1
Правильный многоугольник - вписанный, углы между соседними диагоналями опираются на равные хорды, следовательно равны.
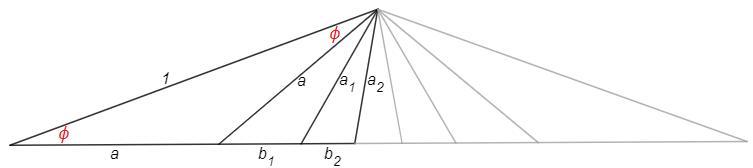
Треугольник A1A2A3 разбит на малые треугольники с равными углами ф при вершине A2 и общей высотой h.
Треугольник со стороной 1 - равнобедренный, углы при основании равны ф (опираются на равные хорды).
sinф =h
S1 = 1/2 aa1 sinф =1/2 b1h => aa1 =b1
Аналогично для любого малого треугольника (a1a2 =b2 ...)
Приложения:
siestarjoki:
Надо понимать, что это выполняется только если A1A2=1
Покорнейше благодарю!
Похожие вопросы
Предмет: Русский язык,
автор: megakasatkin
Предмет: Русский язык,
автор: lera1666666666
Предмет: Русский язык,
автор: виталийканев
Предмет: Математика,
автор: оващь1
Предмет: Биология,
автор: marina198108