Предмет: Алгебра,
автор: oklick1506
найти сумму всех натуральных чисел от 7 до 65
Ответы
Автор ответа:
0
сумма всех натуральных чисел от 7 до 65 это сумма арифмитической прогрессии с первым членом a[1]=7, последним членом a[n]=65 и разницей арифмиттиеческой прогрессии d=1
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
65=7+(n-1)*1
58=n-1
n=58+1=59
по формуле суммы
S=(a[1]+a[n])/2* n
S=(7+65)/2 *59=2 124
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
65=7+(n-1)*1
58=n-1
n=58+1=59
по формуле суммы
S=(a[1]+a[n])/2* n
S=(7+65)/2 *59=2 124
Автор ответа:
0
""""""""""""""""""""""""""""""""""
Приложения:
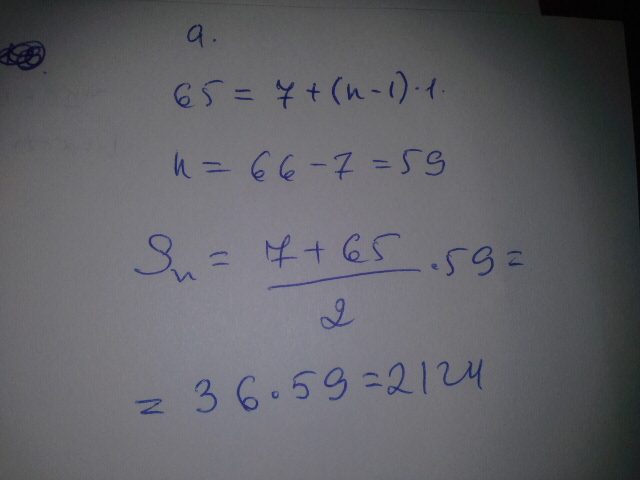
Похожие вопросы
Предмет: Английский язык,
автор: jdjfjfjfjfifid399
Предмет: Математика,
автор: irinadrobkova73
Предмет: Алгебра,
автор: taisiasadqevsnww
Предмет: Математика,
автор: Fima100500