Предмет: Алгебра,
автор: whatspoppinhuh
решите уравнение 3arctg^2x-2piactgx-p^2=0
Приложения:
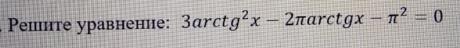
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: 7uykiuol
Предмет: Українська мова,
автор: VIKA0974651642
Предмет: Русский язык,
автор: linalamroeva95
Предмет: Литература,
автор: AselAlima
Предмет: Математика,
автор: egor502