Предмет: Математика,
автор: vicksolovea
метод интегрирования по частям
Приложения:
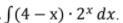
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: 65710
Предмет: Литература,
автор: MrErik118
Предмет: Другие предметы,
автор: sagitova632
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Джеймс1222