Предмет: Геометрия,
автор: lizalolo15
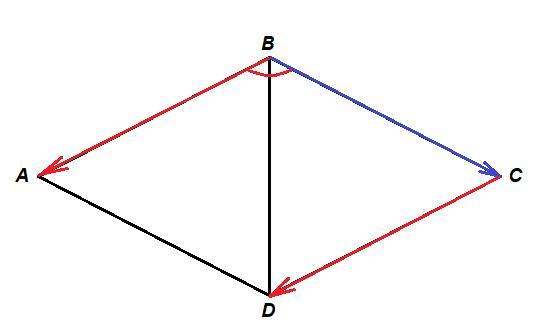
четырехугольник ABCD- ромб. диагональ BD равна стороне ромба. найдите угол между векторами BC и CD. СРОЧНО!!!!
Ответы
Автор ответа:
9
Ответ:
120°
Объяснение:
Если диагональ BD равна стороне ромба, то ΔBCD равносторонний и
∠BCD = 60°.
Сумма углов ромба, прилежащих к одной стороне, равна 180°. Тогда
∠АВС = 180° - ∠BCD = 180° - 60° = 120°
Угол между векторами определен для векторов с общим началом.
Вектор и имеет общее начало с вектором
, значит
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: zverevavalay
Предмет: Литература,
автор: КатяНюша
Предмет: Английский язык,
автор: akbashevaelvin
Предмет: Математика,
автор: VeronikaTyan6661
Предмет: Математика,
автор: alina1234567894