Предмет: Алгебра,
автор: khairov
помогите упр 117(вг) это уравнение буду очень благодарен)
Приложения:
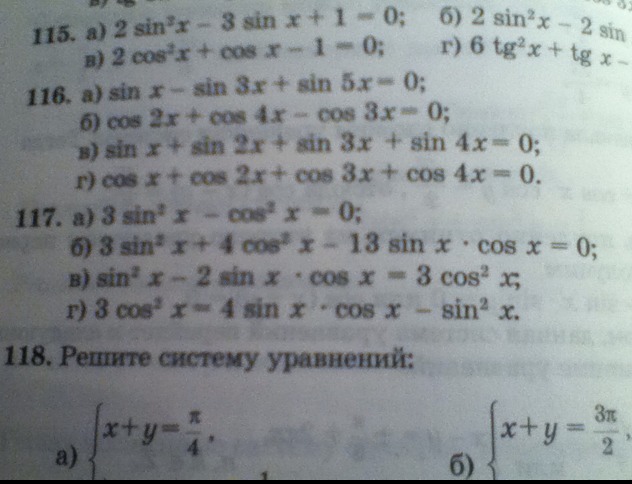
Ответы
Автор ответа:
0
в) sin^2x - 2sinx*cox = 3cjs^2x
sin^2x - 2sinx*cox - 3cjs^2x = 0
Делим всё на cos^2x:
tg^2x - 2tgx - 3 = 0 , tgx=t
t^2 - 2t - 3 = 0
Д=16=4^2
t1=3
t2= -1
tgx1=3
x1=+-arctg3+ n, n∈Z
n, n∈Z
tgx2=-1
x2=-arctg1+ n, n∈Z
n, n∈Z
x2=- /4 +
/4 +  n, n∈Z
n, n∈Z
г) 3cos^2x = 4sinx*cosx - sin^2x
3cos^2x - 4sinx*cosx + sin^2x =0
Делим всё на cos^2x:
3 - 4tgx + tg^2x = 0, tgx=t
t - 4t + 3 = 0
Д=4 = 2^
t1= 1
t2 =4
tgx1=1
x1=+-arctg1 + n, n∈Z
n, n∈Z
x1=+- /4 +
/4 +  n, n∈Z
n, n∈Z
tgx2=4
x2=+-arctg4 + n, n∈Z
n, n∈Z
sin^2x - 2sinx*cox - 3cjs^2x = 0
Делим всё на cos^2x:
tg^2x - 2tgx - 3 = 0 , tgx=t
t^2 - 2t - 3 = 0
Д=16=4^2
t1=3
t2= -1
tgx1=3
x1=+-arctg3+
tgx2=-1
x2=-arctg1+
x2=-
г) 3cos^2x = 4sinx*cosx - sin^2x
3cos^2x - 4sinx*cosx + sin^2x =0
Делим всё на cos^2x:
3 - 4tgx + tg^2x = 0, tgx=t
t - 4t + 3 = 0
Д=4 = 2^
t1= 1
t2 =4
tgx1=1
x1=+-arctg1 +
x1=+-
tgx2=4
x2=+-arctg4 +
Похожие вопросы
Предмет: Английский язык,
автор: sasahasykhareva
Предмет: Математика,
автор: 1333568767897
Предмет: Физика,
автор: oksanaroztoku071
Предмет: Биология,
автор: ALINATR0806