Предмет: Алгебра,
автор: GreenMonster7
Ребята помогите алгебра
Скорей
Приложения:
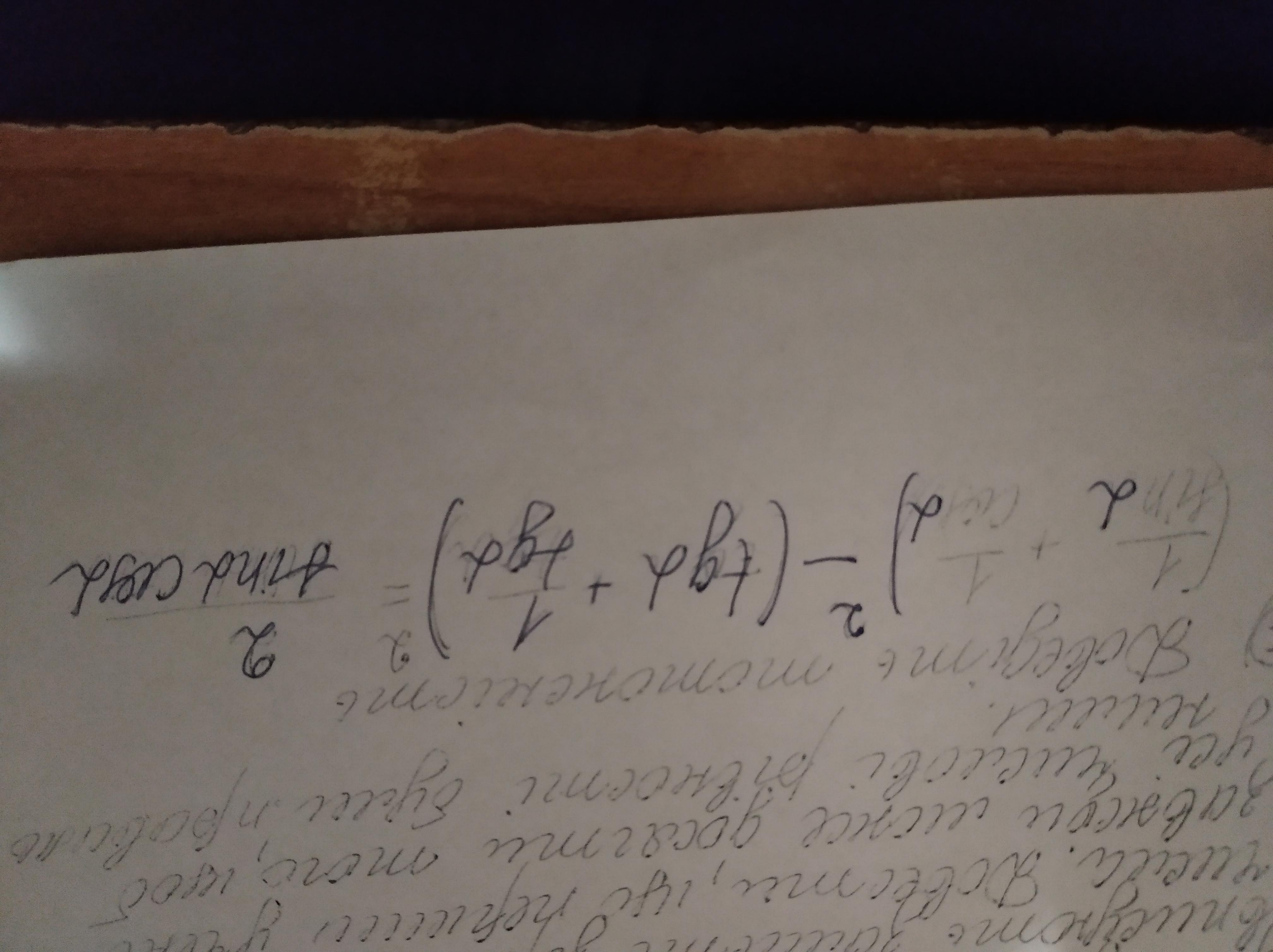
Ответы
Автор ответа:
1
Доказано
GreenMonster7:
Спасибі огромноє
Похожие вопросы
Предмет: Физика,
автор: йцукенгшщзхъё1234567
Предмет: Алгебра,
автор: syperdima1
Предмет: Қазақ тiлi,
автор: ilia29
Предмет: Математика,
автор: milisa2106