Question

Геометрия,очень нужно.Спасибо!
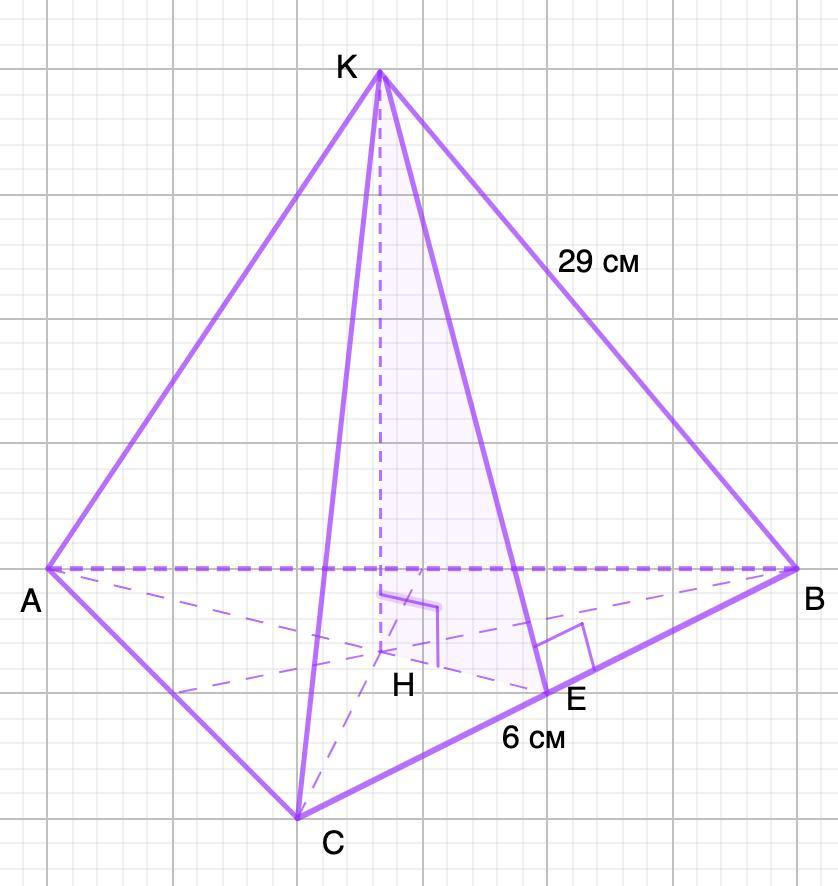
а)Нарисуйте изображение правильной треугольной пирамиды. Изобразите апофему и высоту пирамиды.
б)Сторона основнання правильной треугольной пирамиды равна 6 см, а боковое ребро —

29 см. Найдите высоту пирамиды,​

Answer 1

Ответ:

КН=√829 см

Объяснение:

• а) Правильная треугольная пирамида — это пирамида с правильным треугольником в основании, а грани - равнобедренные треугольники).

ΔАВС - равносторонний треугольник;

ΔАКС, ΔСКВ, ΔАКВ - равнобедренные треугольники.

• Высота боковой грани правильной пирамиды называется апофемой.

КЕ - апофема

• Высота пирамиды - это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

КН - высота.

Н - точка пересеченич медиан (биссектрис, высот) основания.

б) Дано: КАВС - правильная пирамида.

СВ=6 см; СВ = 29 см.

Найти: КН.

Решение:

1. Рассмотрим ΔСКВ - равнобедренный.

В равнобедренном треугольнике высота является медианой

⇒КЕ - апофема, то есть высота, медиана.

СЕ=ЕВ=6:2=3 (см)

Рассмотрим  ΔЕКВ - прямоугольный.

По теореме Пифагора:

КЕ²=КВ²-ЕВ²

КЕ²=841-9=832 или КЕ=√832 (см)

Рассмотрим ΔАВЕ - прямоугольный.

По теореме Пифагора:

АЕ²=АВ²-ЕВ²

АЕ²=36-9=27 или АЕ=√27=3√3 (см)

• Медианы точкой пересечения делятся в отношении 2:1, считая от вершины.

⇒ НЕ=АЕ:3  

НЕ=3√3:3=√3 (см)

Рассмотрим ΔНКЕ - прямоугольный.

По теореме Пифагора:

КН²=КЕ²-НЕ²

КН²=832-3=829 или КН=√829 (см)