Question

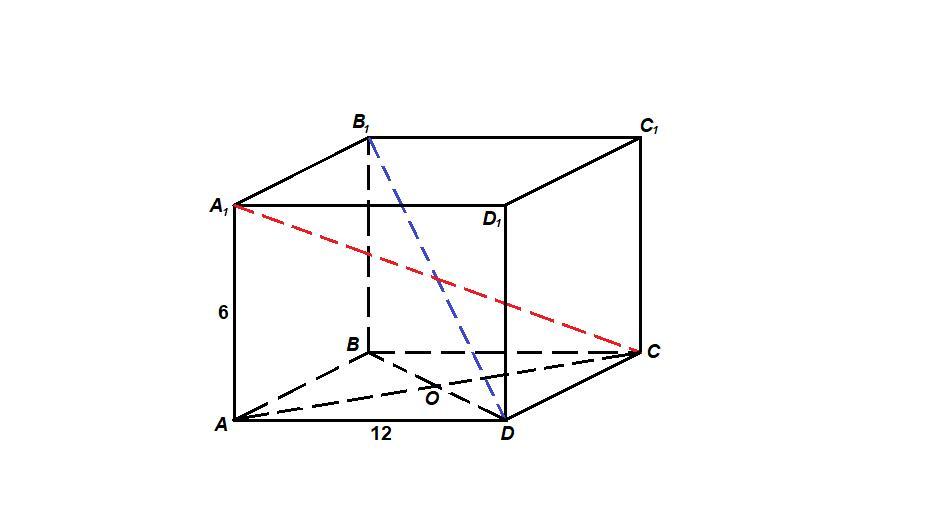
В основании прямой призмы лежит ромб с тупым углом 120° и стороеой 12см. Найти диагонали призмы, если ее боковое ребро равно 6 см.​

Answer 1

Ответ:

6√13 см и 6√5 см

Объяснение:

Сумма соседних углов ромба равна 180°. Так как по условию ∠АВС = 120°, то

∠BAD = 180° - 120° = 60°

ΔBAD равнобедренный (АВ = AD как стороны ромба) с углом 60°, значит он равносторонний,

BD = АВ = 12 см

ΔBB₁D:  ∠B₁BD = 90°, то теореме Пифагора

  B₁D = √(BB₁² + BD²) = √(6² + 12²) = √(36 + 144) = √180 = 6√5 см

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Тогда АО - высота равностороннего треугольника ABD.

АО = АВ√3/2 = 12√3 / 2 = 6√3 см

АС = 2АО = 12√3 см

ΔАА₁С:  ∠А₁АС = 90°, по теореме Пифагора

  А₁С = √(АА₁² + АС²) = √(6² + (12√3)²) = √(36 + 423) = √468 = 6√13 см