Предмет: Геометрия,
автор: laminnt1324
СРОЧНО
В разных сторонах от прямой даны точки A и B на расстояниях 8,3 см и 4,5 см от прямой соответственно.
Определи расстояние серединной точки C отрезка AB до прямой.
Ответы
Автор ответа:
5
Ответ:
1,9 cм
Объяснение:
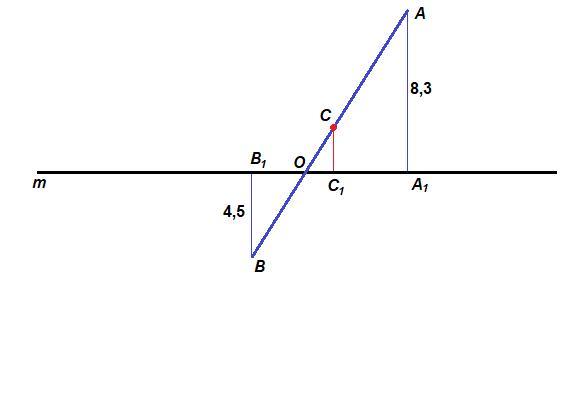
Из точек А, В и С проведем перпендикуляры к прямой m: АА₁, ВВ₁ и СС₁.
АА₁ = 8,3 см
ВВ₁ = 4,5 см
СС₁ - ?
ΔАА₁О подобен ΔВВ₁О по двум углам (∠АА₁О = ∠ВВ₁О = 90°, углы при вершине О равны как вертикальные), значит
Тогда отрезок АВ составляет
45 + 83 = 128 частей и
, так как С - середина АВ.
ΔАА₁О подобен ΔCC₁О по двум углам (∠АА₁О = ∠CC₁О = 90°, угол при вершине О общий), значит
см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: iryskaaa
Предмет: Английский язык,
автор: mak116
Предмет: Геометрия,
автор: dilshoda38
Предмет: Математика,
автор: эми41