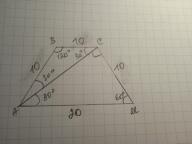
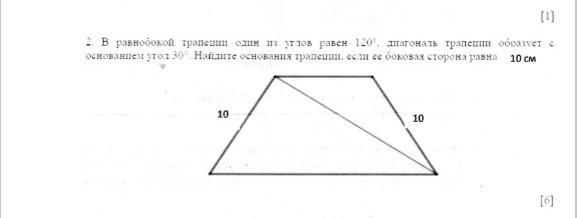
В равнобокой трапеции один из углов равен 120°,диагональ трапеции образует с основание угол 30°.Найдите основания трапеции,если ее боковая сторона равна 10 см
Ответы
Ответ:
50 см
Объяснение:
Дано: АВСМ - трапеция, АВ=СМ=10 см, ∠САМ=30°; ∠В=120°, Найти Р(АВСМ).
Сумма углов трапеции, прилежащих к боковой стороне, составляет 180°.
∠ВАМ=180-120=60°.
∠ВАС=60-30=30°, ∠ВСА=180-(120+30)=30°, значит, ΔАВС - равнобедренный, ВС=АВ=СМ=10 см.
ΔАСМ - прямоугольный, ∠С=180-(60+30)=90°
СМ=1/2 АМ как катет, лежащий против угла 30°
АМ=10*2=20 см
Р=10+10+10+20=50 см