Question

помогите пж срочно
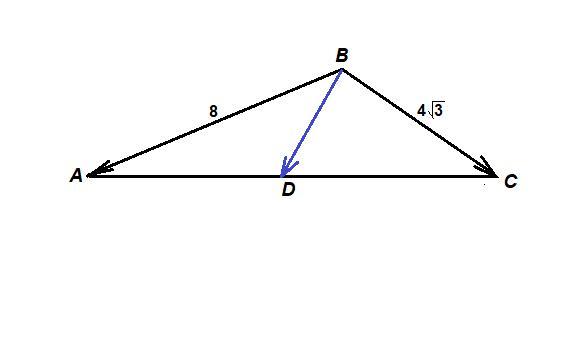
Дан треугольник ABC. Известно, что AB = 8, BC = 4 корень 3
, ∠ABC = 150°. Найди длину медианы BD. Реши задачу, применяя векторы.

Answer 1

Ответ:

2

Объяснение:

Рассмотрим векторы $\overrightarrow{BA}$ и $\overrightarrow{BC}$.

Так как D - середина отрезка АС, то

$\overrightarrow{BD}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)$

Возведем в квадрат обе части равенства:

$\overrightarrow{BD}^2=\dfrac{1}{4}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)^2$

$|\overrightarrow{BD}|^2=\dfrac{1}{4}\left(\overrightarrow{BA}^2+2\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{BC}^2\right)=$

$=\dfrac{1}{4}\left(|\overrightarrow{BA}|^2+2\overrightarrow{BA}\cdot \overrightarrow{BC}+|\overrightarrow{BC}|^2\right)$

$|\overrightarrow{BA}|=8$

$|\overrightarrow{BC}|=4\sqrt{3}$

$\overrightarrow{BA}\cdot \overrightarrow{BC}=|\overrightarrow{BA}|\cdot |\overrightarrow{BC}|\cdot \cos \angle ABC=8\cdot 4\sqrt{3}\cdot \cos 150^\circ=32\sqrt{3}\cdot \left(-\dfrac{\sqrt{3}}{2}\right)=-48$

$|\overrightarrow{BD}|^2=\dfrac{1}{4}\left(8^2+2\cdot (-48)+(4\sqrt{3})^2\right)=$

$=\dfrac{1}{4}\left(64-96+48\right)=\dfrac{1}{4}\cdot 16=4$

$BD=\sqrt{4}=2$