Question

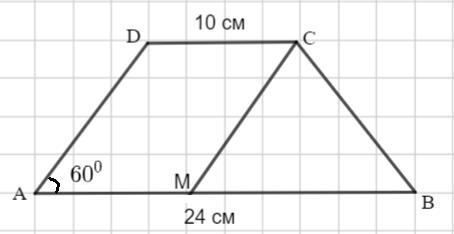
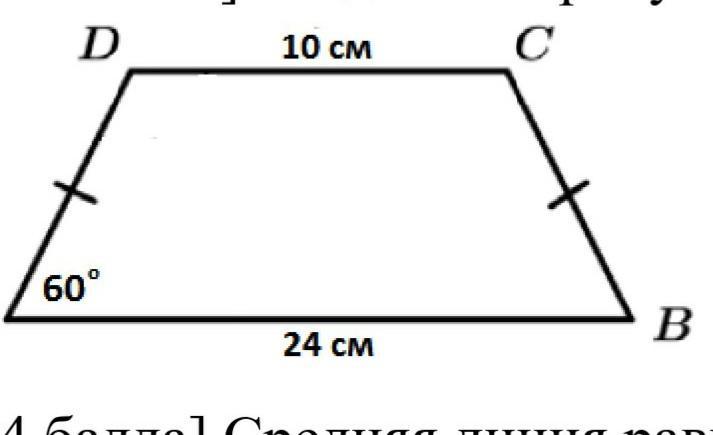
По данным рисунка найдите периметр трапеции





​

Answer 1

Ответ:

62 см

Объяснение:

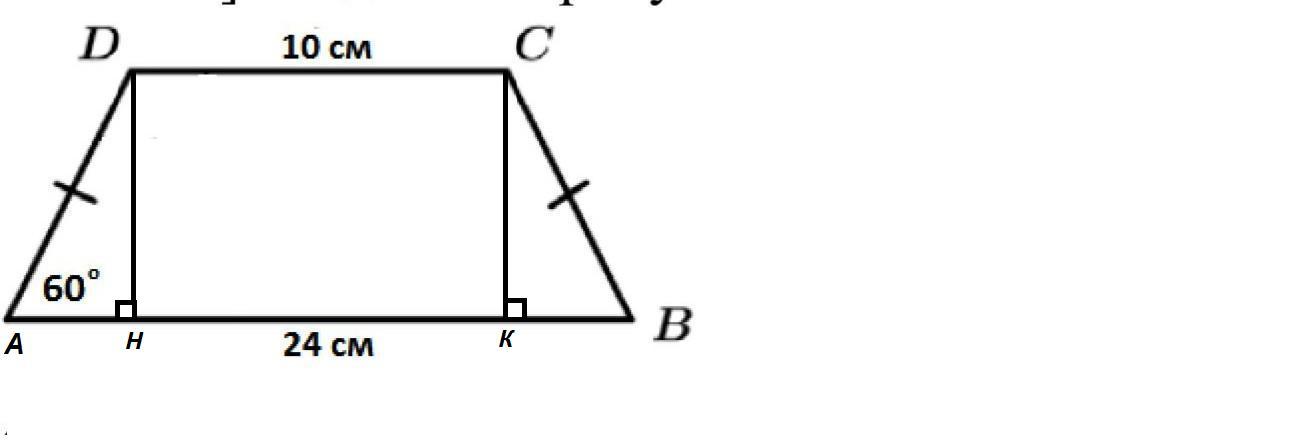
Проведем высоты DH и СК.

HDCK - прямоугольник, так как все углы прямые.

НК = DC = 10 см

ΔADH = ΔBCK по гипотенузе и катету:

• ∠AHD = ∠BKC = 90°;
• AD = CB по условию;
• DH = CK как высоты трапеции.

$AH=BK=\dfrac{AB-HK}{2}=\dfrac{24-10}{2}=\dfrac{14}{2}=7$ см

ΔADH:   ∠AHD = 90°,  ∠A = 60°,

    ∠ADH = 90° - ∠A = 90° - 60° = 30°

    AD = 2 · AH = 2 · 7 = 14 см по свойству катета, лежащего против угла в 30°.

СВ = AD = 14 см

Периметр трапеции:

P = AB + DC + 2 · AD = 24 + 10 + 2 · 14 =34 + 28 = 62 см

Answer 2

Ответ:

Р=62 см.

Объяснение:

В равнобедренной трапеции ABCD.

AB= 24см,  DC=10 cм.

∠А=∠В=60°.

Проведем СМ║AD.

Тогда ADCM - параллелограмм, так как противолежащие стороны попарно параллельны.

∠СМВ = ∠DAB как соответственные при AD║CM и секущей АВ.

AD=CM,  как противолежащие стороны параллелограмма.

Тогда в равнобедренном треугольнике МСВ

∠СМВ=∠МВС= 60°. Тогда ∠МСВ =60° и ΔМСВ  - равносторонний.

DC=AM =10 cм, как противолежащие стороны параллелограмма.

МВ =24 - 10= 14 см .

Тогда  СВ = МВ=14 см.

В равнобедренной трапеции AD= CB= 14 см.

Периметр трапеции - это сумма длин всех сторон.

P=AD+DC+CB+AB;

P=14+10+14+24=24+38=62 cм