Предмет: Алгебра,
автор: aizirekdoronbekova9
На оси ординат найти точку равноудаленную от точек C(4:-3)и D(8:1)
Ответы
Автор ответа:
4
Ответ:
A(0; 5)
Объяснение:
Обозначим искомую точку через A;
Поскольку по условию она лежит на оси ординат, её координаты (0 ; y);
;
Так как по условию задачи эти расстояния равны, составим равенство
AC = AD и решим его:
| избавимся от корней, возведя обе части в квадрат;
8y = 40
y = 5
Следовательно A(0; 5)
Автор ответа:
4
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!
Приложения:

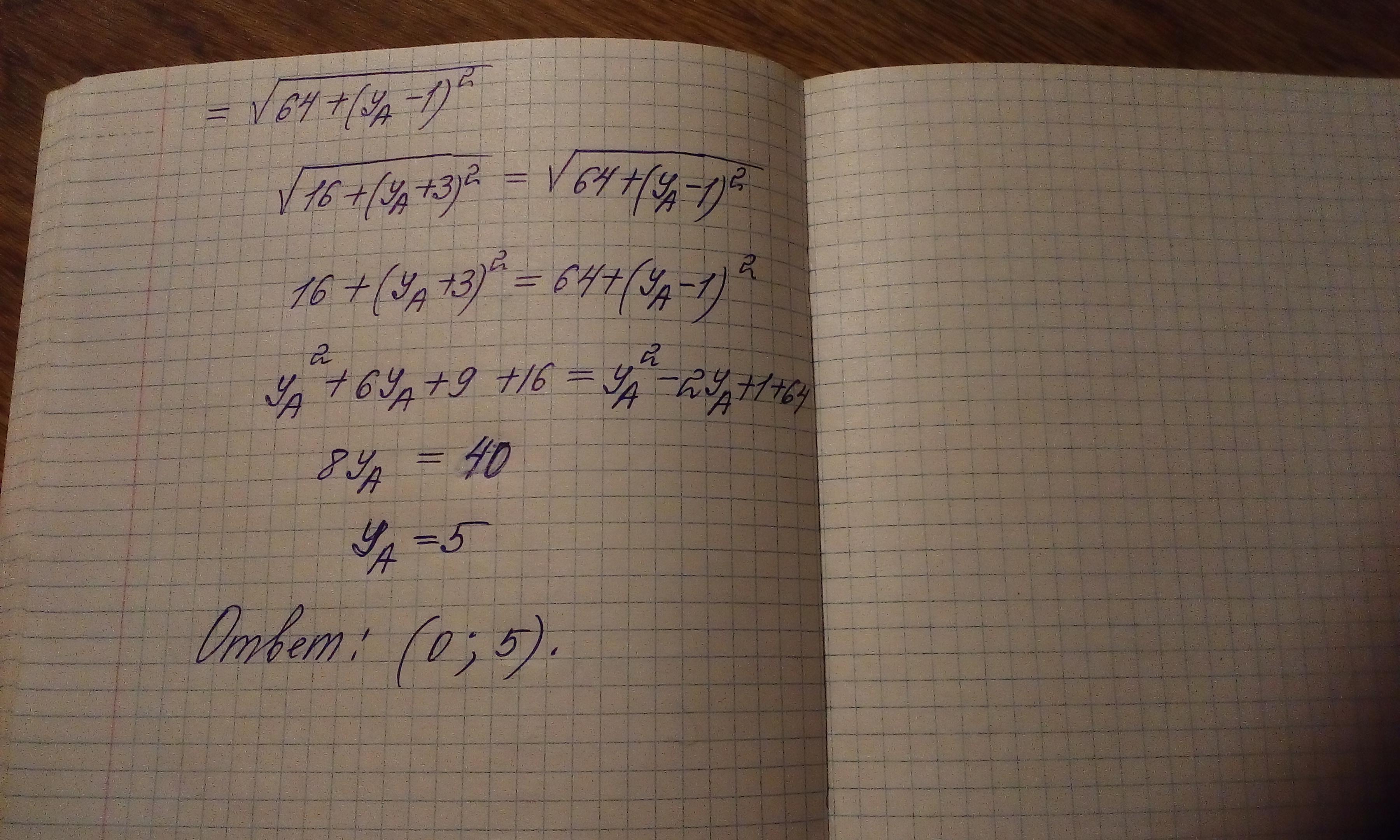
Похожие вопросы
Предмет: Английский язык,
автор: maksimfazlyev04
Предмет: Русский язык,
автор: storatex1
Предмет: Українська мова,
автор: daryatymchuk
Предмет: Литература,
автор: Жучка11
Предмет: Математика,
автор: marinagor2012