Предмет: Алгебра,
автор: Diamantid1
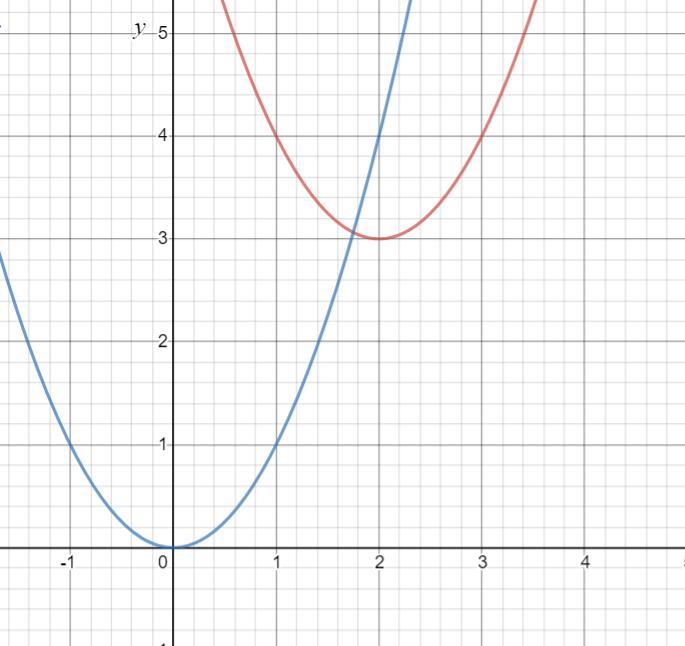
С помощью параболы y=x^2 постройте график функции
y=x^2−4x+7, выделив полный квадрат. Найдите множество значений функции и укажите промежутки монотонности.
Ответы
Автор ответа:
2
Объяснение:
Выделим полный квадрат:
x²- 4x + 7 = x² - 2·2·x + 4 + 3 = (x-2)² + 3
Таким образом, график функции y = x²- 4x + 7 получается смещением графика y = x²
на 3 вверх по оси OY
на 2 вправо по оси OX
Множество значений:
E(y) = [3; +∞)
Такая функция:
убывает на промежутке (-∞; 2)
возрастает на промежутке (2; +∞)
Приложения:
mishsvyat:
Дополнил множество значений и промежутки монотонности
Похожие вопросы
Предмет: Русский язык,
автор: kartoon
Предмет: Другие предметы,
автор: alexarikova
Предмет: Русский язык,
автор: egoryanko07
Предмет: География,
автор: Даниил739294739
Предмет: География,
автор: anna997171