Предмет: Математика,
автор: 1RearceMercury0
Кто поможет решить предел?
Приложения:
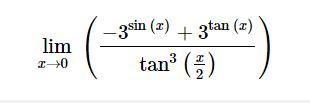
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
__________________
в окрестности точки , где
- бесконечно малая функция в этой окрестности
Похожие вопросы
Предмет: Українська мова,
автор: aleksandracawa
Предмет: Русский язык,
автор: Алина12111
Предмет: Русский язык,
автор: anyyyyy
Предмет: Математика,
автор: Z3t