Предмет: Алгебра,
автор: upimn
Упростите выражение:
Приложения:
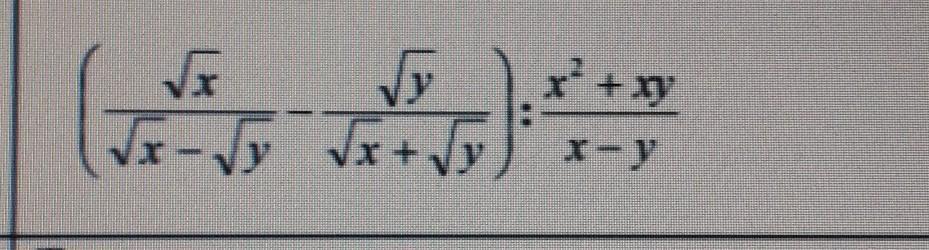
Ответы
Автор ответа:
1
Ответ:
upimn:
Пасиба
Похожие вопросы
Предмет: Русский язык,
автор: soloniy2013
Предмет: Английский язык,
автор: РэмКрасный
Предмет: Английский язык,
автор: iksenia1405
Предмет: Литература,
автор: Genius4432
Предмет: Математика,
автор: phakim