Question

1) Длина прямоугольника втрое больше его ширины. После того как длину прямоугольника увеличили на 5 см, а ширину - на 10см, его площадь увеличилась в 4 раза. Найдите периметр первоначального прямоугольника. 

Answer 1

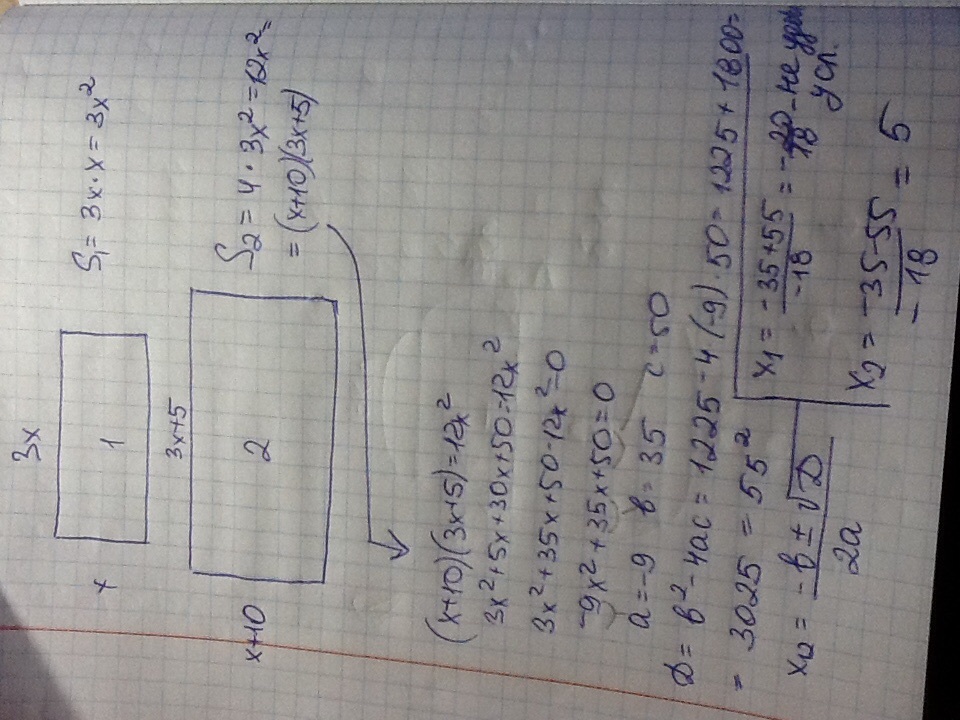
Для начала начертим два прямоугольника. Обозначим за х - первую ширину, тогда
3х- первая длина,
х+10 - вторая ширина,
а 3х+5 - вторая длина.

S1=3х*х=3х², a S2=(x+10)(3x+5).
Но по условию S2=4S1=4*3x²=12x². Составим уравнение.

Дальше - смотрим на фото. Раскрыв скобки и приведя подобные, мы, наконец, дошли, до квадратного полного уравнения, решать которое мы будем через Дискриминант.

х1 нам не подходит, так как длина не может быть отрицательной.
Первоначальный периметр = 3х+х+3х+х=8х=8*5=40 см.

Ответ: 40 см.