Предмет: Математика,
автор: ukguchi
Помогите решить пределы ❤️
Приложения:
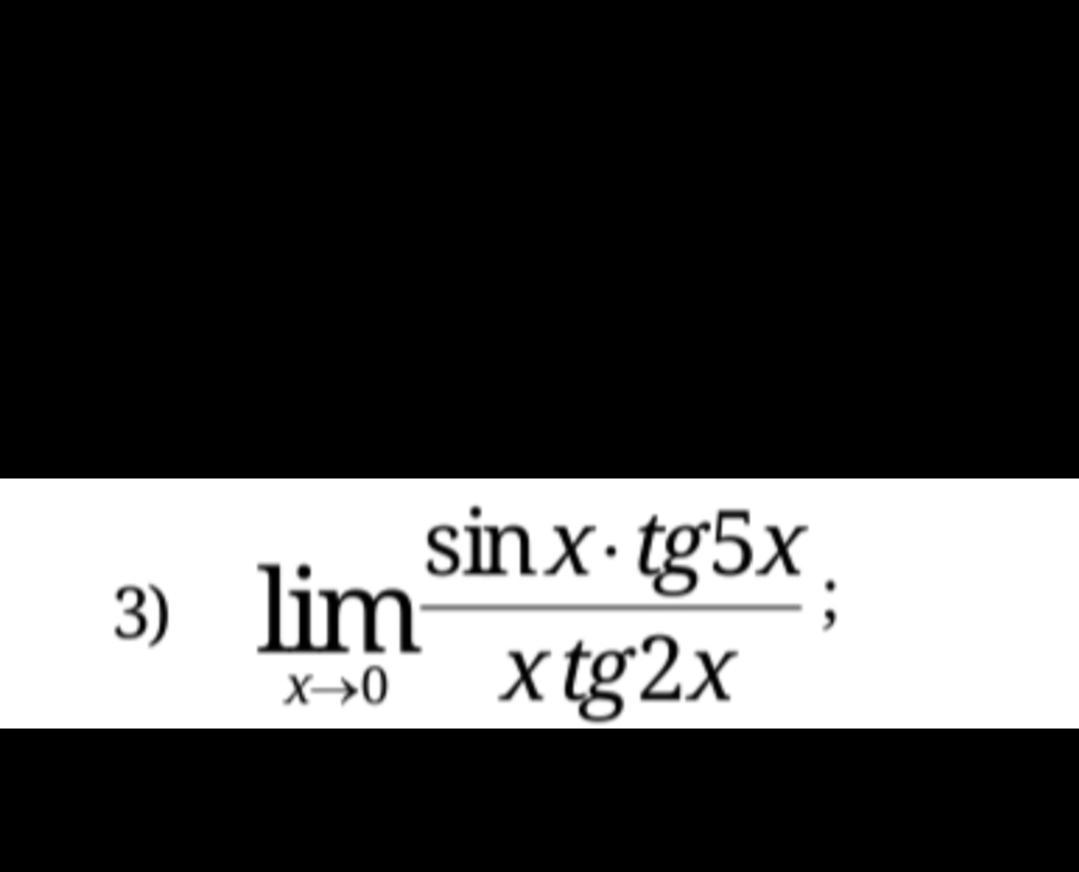
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: ak2002
Предмет: Русский язык,
автор: LeshaAgent007
Предмет: Русский язык,
автор: marjanka04
Предмет: История,
автор: nikitafirsov473