Предмет: Геометрия,
автор: tigrlena
ПОМОГИТЕ!!!
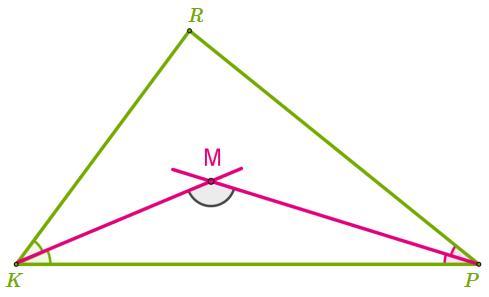
Дан треугольник KRP и биссектрисы углов ∡ PKR и ∡ RPK.
Определи угол пересечения биссектрис ∡ KMP, если ∡ PKR = 52° и ∡ RPK = 68°.
∡ KMP = °.
Приложения:
tigrlena:
ПОМОГИТЕ ПОМОГИТЕ ПОМОГИТЕ
Ответы
Автор ответа:
0
Ответ:
130
Объяснение:
угол КМР =52/2=26, ТК КМ- биссектриса.
угол МРК=68/2=34,тк. РМ- биссектриса.
Рассмотрим треугольник КМР. ТК сумма углов треугольника равна 180, то угол М=180-(26+34)=120. Ответ :120°.
Автор ответа:
0
Ответ: ∡ KMP = 120°.
Объяснение:
∠ RKM=∠MKP=52°/2=26°;
∠RPM=∠MPK=68°/2=34°;
∠KMP=180°-(26°+34°)=180°-60°=120°.
Похожие вопросы
Предмет: Русский язык,
автор: Lalka180
Предмет: Другие предметы,
автор: kovrik911
Предмет: Другие предметы,
автор: лера62
Предмет: Математика,
автор: Vinokurowayeka
Предмет: Математика,
автор: Helpmeplz123