Question

Стороны треугольника равны 5 см, 7 см и 10 см.Найдите медиану,проведённую к большей стороне.

Answer 1

Ответ:

Mа = 2√3 см.

Объяснение:

По формуле медианы:

Ma = (1/2)·√(2b²+2c²-a²).

В нашем случае a = 10 см, b = 5 cм, с = 7 см.

Ma =  (1/2)·√(50+98-100) = (√48)/2 = (2√12)/2 = √12 = 2√3 cм.

Или так:

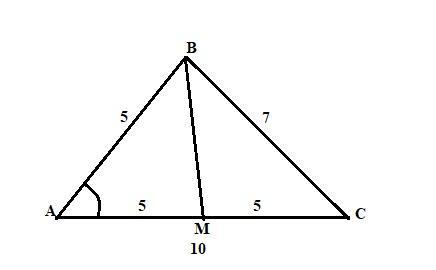
Пусть дан треугольник АВС, в котором АВ = 5 см, ВС = 7 см и АС = 10 см.

Проведена медиана ВМ. АМ = МС = 5 см.

По теореме косинусов для угла А  в треугольнике АВС имеем:

CosA = (AB²+BC²-AC²)/(2·AB·AC) = (100+25-49)/100 = 0,76.

По теореме косинусов для угла А  в треугольнике АВМ имеем:

ВМ² = АВ²+АМ² - 2·АВ·АМ·СоsА = 25 + 25 - 2·5·5·0,76 = 12.

ВМ = √12 = 2√3 см.