Предмет: Алгебра,
автор: au456
Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости .
Приложения:
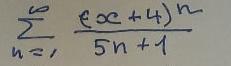
valkerimova33:
Ты главный модератор че вопросы задаешь и?
Ответы
Автор ответа:
3
А значит интервал сходимости
Исследуем на концах:
расходится, как гармонический - а тогда, согласно предельному признаку сравнения,
также расходится
1)
2) , а значит
монотонно убывает
3)
А тогда, по признаку Лейбница, сходится
А значит ряд сходится на
Еще наверное стоит добавить что при -5 условно сходится - ну и интервал конечно [-5;-3) , а не как написано ))
Вот сидел вспоминал сегодня ))
Нет, при исследовании на сходимости тип не указывается.
Вот если бы нужно было исследовать на абсолютную сходимость - тогда да)
Вот если бы нужно было исследовать на абсолютную сходимость - тогда да)
Да, с интервалом я ошибся) Спасибо, исправил
Если все знаешь зачем вопрос задаешь?
Похожие вопросы
Предмет: Русский язык,
автор: nazaryannaira1
Предмет: Українська мова,
автор: tnagig
Предмет: Русский язык,
автор: elistratovavera
Предмет: Математика,
автор: 90Лилиана11111
Предмет: Математика,
автор: дождливый