Предмет: Алгебра,
автор: au456
Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости .
Приложения:
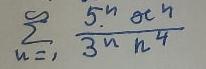
Ответы
Автор ответа:
3
А значит интервал сходимости
Исследуем на концах:
- сходится как обобщенный гармонический ряд с
Заметим, что ряд из модулей сходится (по доказанному ранее). А значит и ряд
сходится
А тогда исходный ряд сходится на
au456:
Спасибр ! Уже пришлось вспомнить как это делается ))
Похожие вопросы
Предмет: Русский язык,
автор: elistratovavera
Предмет: Беларуская мова,
автор: ratno30
Предмет: Другие предметы,
автор: krupenkovakate
Предмет: Математика,
автор: ДашаШирова
Предмет: Математика,
автор: saaaat