Question

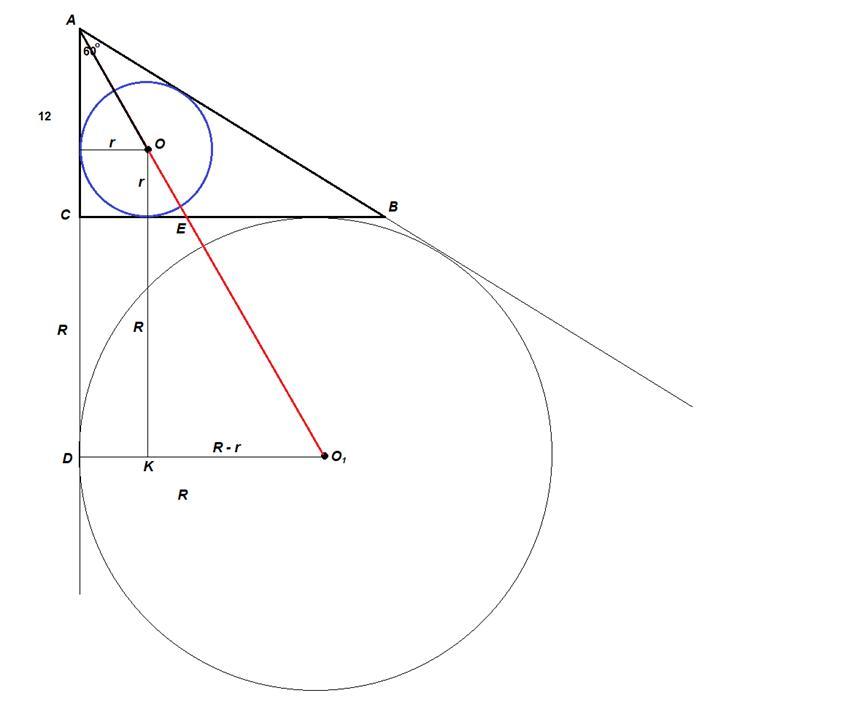
Дан прямоугольный треугольник ABC, в котором угол A =60, угол С =90. Известно, что AC=12. Чему равно расстояние между центрами его вписанной окружности I и вневписанной окружности Ia, касающейся стороны BC?​

Answer 1

Ответ:

24

Объяснение:

Все для ΔABC:

∠C = 90°,  ∠A = 60°, ⇒ ∠B = 30°,  ⇒

AB = 2AC = 24,

BC = AB · sin∠A = 24 · √3/2 = 12√3

Радиус окружности, вписанной в прямоугольный треугольник:

r = p - c

где р - полупериметр, с - гипотенуза.

p = (24 + 12 + 12√3)/2 = (36 + 12√3)/2 = 18 + 6√3

r = 18 + 6√3 - 24 = 6√3 - 6

Центр вписанной окружности - точка О - точка пересечения биссектрис.

Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

$\dfrac{CE}{EB}=\dfrac{AC}{AB}=\dfrac{12}{24}=\dfrac{1}{2}$

$\boldsymbol{CE}=\dfrac{1}{3}BC\boldsymbol{=4\sqrt{3}}$

__________________________

Центр - точка О₁ - вневписанной окружности, касающейся стороны ВС, лежит на биссектрисе противолежащего угла (свойство вневписанной окружности).

Итак, АО₁ - биссектриса угла А, точка О лежит на ней.

Проведем O₁D - радиус в точку касания, O₁D⊥AC.

ΔАСВ ~ ΔADO₁ по двум углам (прямоугольные, ∠А общий),

$\dfrac{CE}{DO_1}=\dfrac{AC}{AD}$

$\dfrac{4\sqrt{3}}{R}=\dfrac{12}{12+R}$

12R = 48√3 + 4√3R

4R(3 - √3) = 48√3

R√3(√3 - 1) = 12√3

R(√3 - 1) = 12

$\boldsymbol{R}=\dfrac{12}{\sqrt{3}-1}=\dfrac{12(\sqrt{3}+1)}{2}\boldsymbol{=6\sqrt{3}+6}$

_______________________________

KO₁ = R - r = 6√3 + 6 - (6√3 - 6) = 12

KO = R + r = 6√3 + 6 + 6√3 - 6 = 12√3

ΔO₁KO = ΔACB по двум катетам,  ⇒

OO₁ = AB = 24