Предмет: Математика,
автор: flanser1
помогите пожалуйста решить
Приложения:
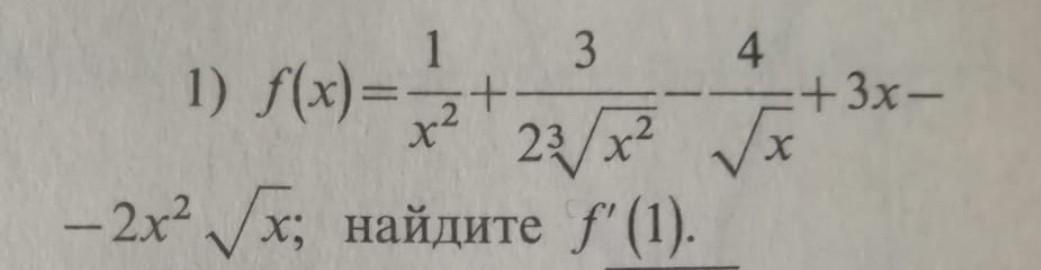
Ответы
Автор ответа:
1
Ответ:
f'(x) = -1,75
Решение:
Производная суммы равна сумме производных
Похожие вопросы
Предмет: Русский язык,
автор: Bylyn
Предмет: Другие предметы,
автор: ccuduxtudycx7
Предмет: Английский язык,
автор: ttonik1711
Предмет: География,
автор: Владос1324
Предмет: Математика,
автор: Vadimoskii