Предмет: Математика,
автор: dimakonstatinopolsky
ДАЮ МАКС.БАЛЛ
ПОЖАЛУЙСТА СРОЧНО
Приложения:
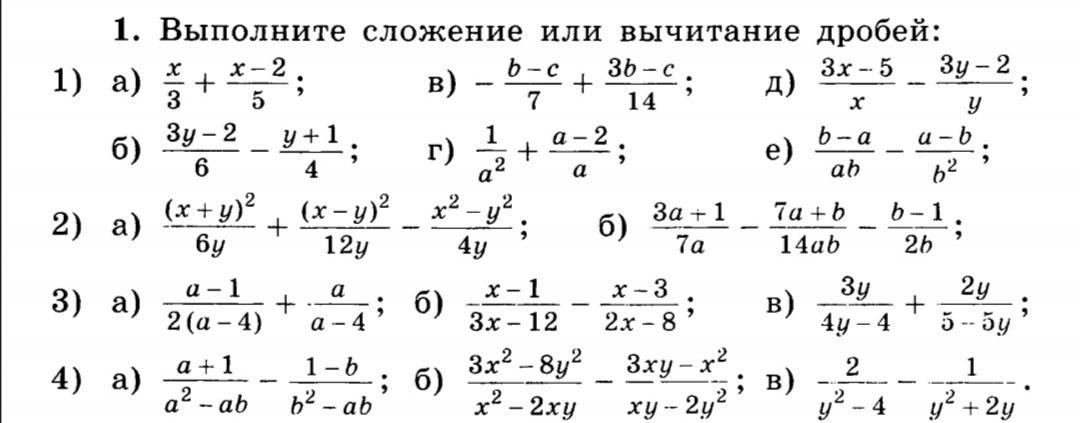
dimakonstatinopolsky:
полное пожалуй
Ответы
Автор ответа:
3
Ответ: 1)
а)
б)
в)
г)
д)
е)
2)
a)
б)
спасибо
Автор ответа:
2
решение на фотографиях
Приложения:
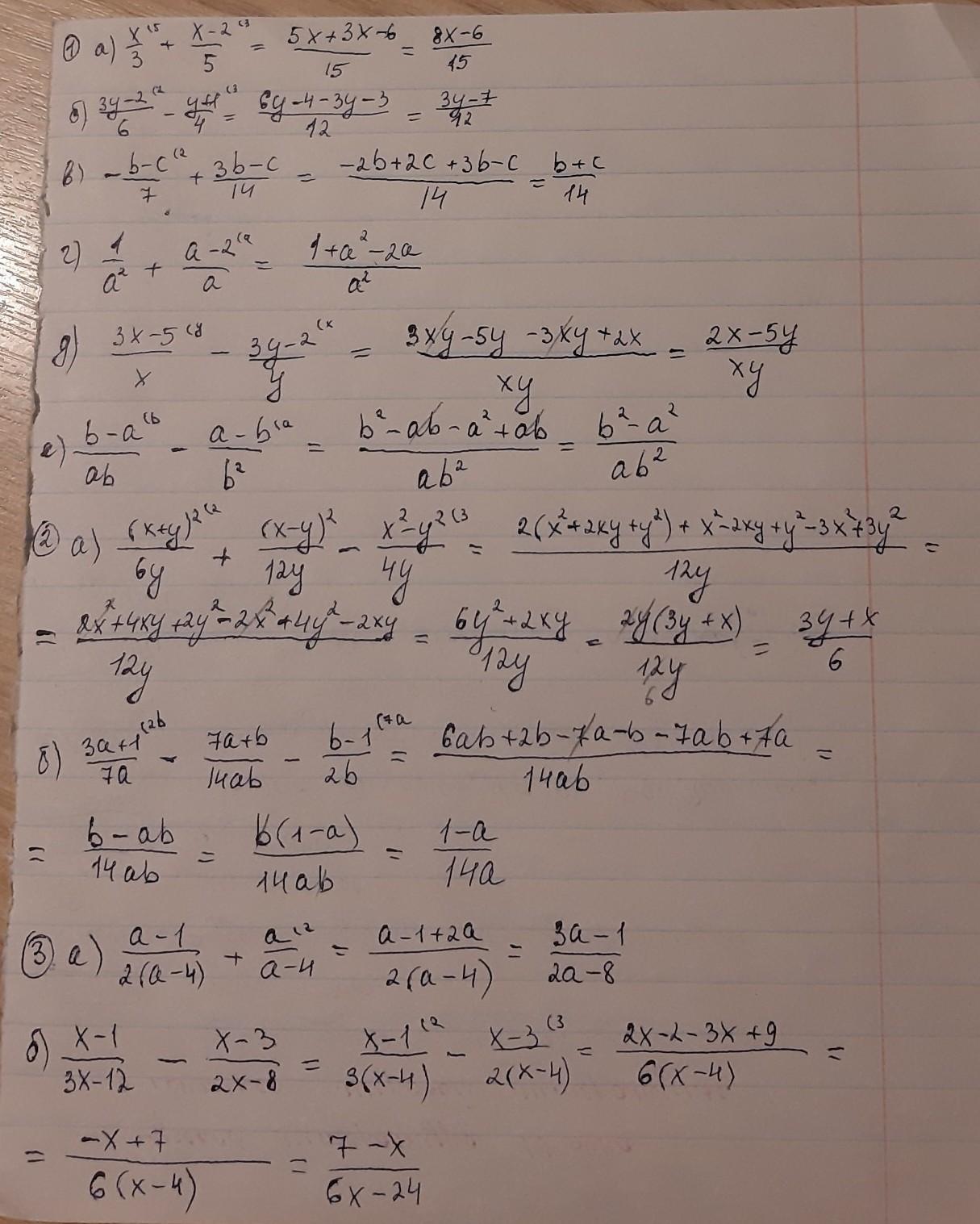
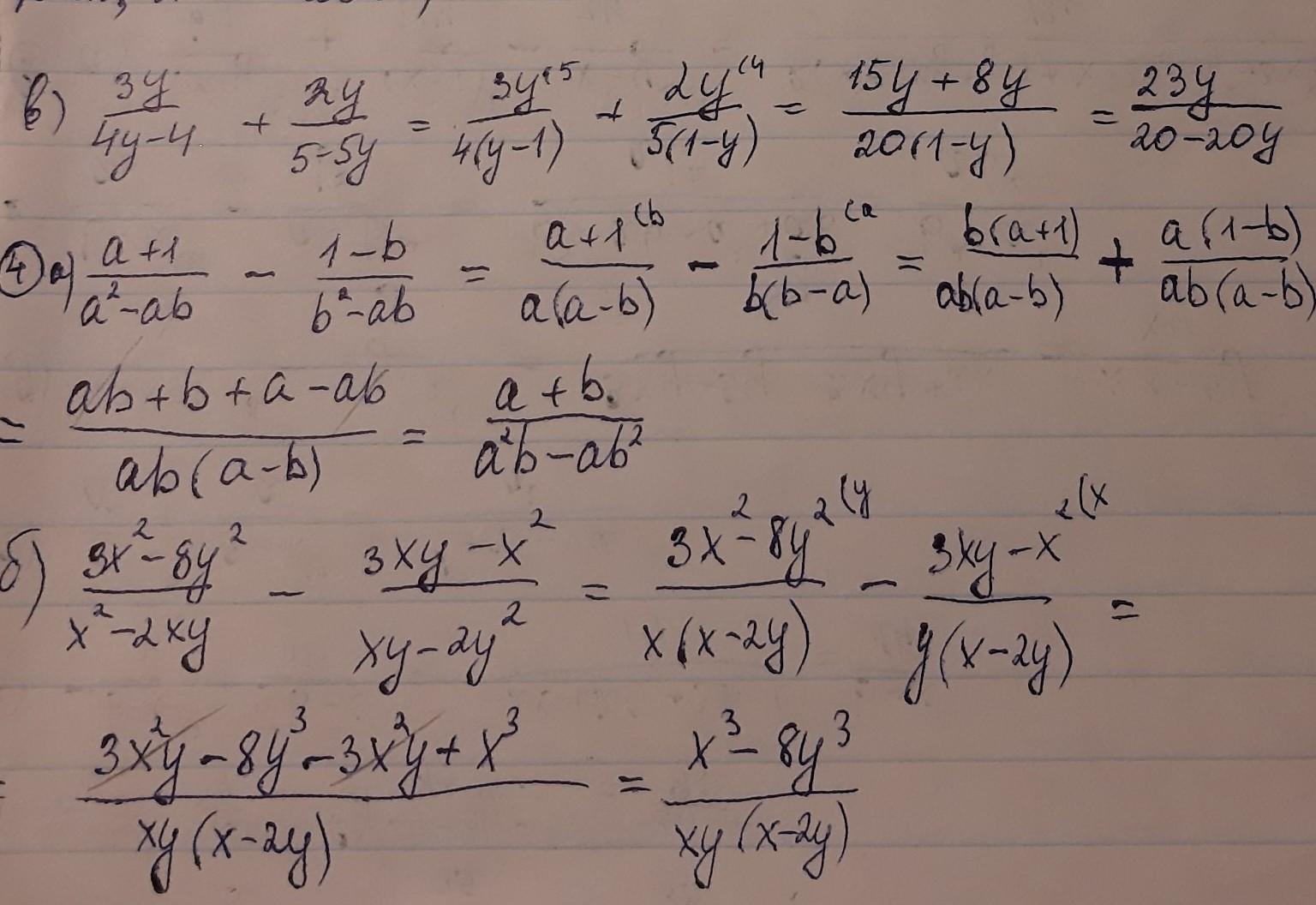

спасибо вам
Похожие вопросы
Предмет: Другие предметы,
автор: tarabarinandrei
Предмет: Другие предметы,
автор: afonya1122
Предмет: Другие предметы,
автор: trtrtrtrtrt
Предмет: Математика,
автор: Damisok