Предмет: Математика,
автор: МаДиНаДАГ
мат анализ. Доказать равенство. Помогите пожалуйста
Приложения:
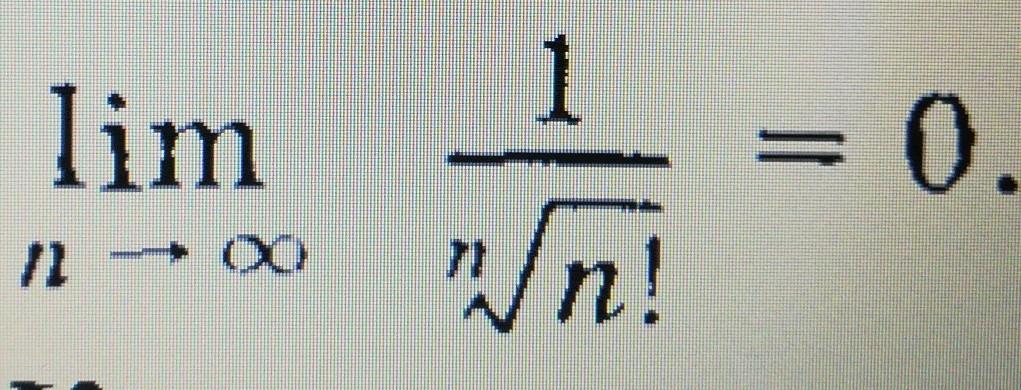
lidiasaraa3:
ошибка в условии
уже нет)
Ответы
Автор ответа:
0
Для начала докажем неравенство методом математической индукции. При n = 1 неравенство имеет место. Далее, если оно имеет место при n, то для n+1 имеем
Последнее неравенство справедливо, так как
Существование и равенство нулю предела вытекает из неравенства
справедливого
при всех
.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: vipegor1712
Предмет: Русский язык,
автор: alex161ru
Предмет: Алгебра,
автор: ангелок163
Предмет: История,
автор: Sona338