Предмет: Математика,
автор: МаДиНаДАГ
Мат анализ. Доказать равенство
Приложения:
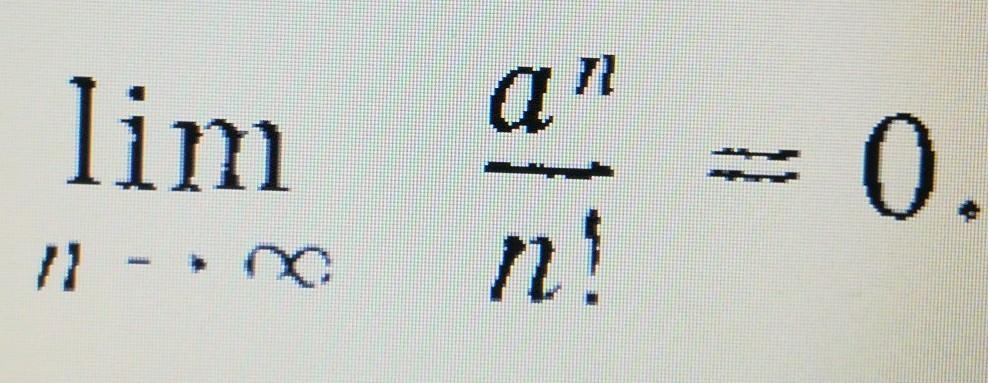
Ответы
Автор ответа:
0
Ответ: 0
Пошаговое объяснение:
Равенство нулю предела следует из очевидного неравенства
справедливого и при
, если
достаточно велико.
Похожие вопросы
Предмет: Русский язык,
автор: lubovdanil
Предмет: Русский язык,
автор: burichdi
Предмет: Английский язык,
автор: nobodyknows0066
Предмет: География,
автор: лишенка
Предмет: Математика,
автор: алиярсик