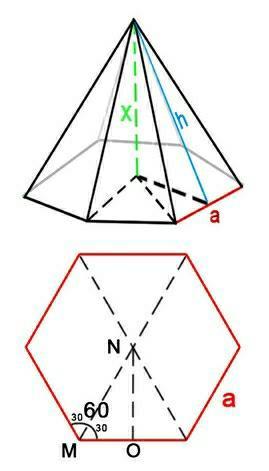
Вычислите площадь поверхности правильной шестиугольной пирамиды ребро основания которой 3см а апофема 5см
Ответы
Ответ:
Sпол=13,5√3+45≈68,355см²
Объяснение:
Полная площадь поверхности пирамиды состоит и суммы площадей её боковой поверхности и основания. Так как её апофема перпендикулярна ребру основания мы найдём площадь её боковой грани по формуле площади треугольника, поскольку боковая грань пирамиды - это равнобедренный треугольник: S=½×a×h, где в нашем случае а- это сторона боковой грани, а h -высота (апофема) которая проведена к стороне:
Sбок.гр=½×3×5=15÷2=7,5см²
Так как таких граней 6 то площадь боковой поверхности пирамиды составит: Sбок.пов=7,5×6=45см²
Теперь найдём площадь основания. Правильный шестиугольник состоит из 6-ти правильных треугольников со стороной 3см. Площадь правильного треугольника вычисляется по формуле:
S=(a²√3)/4 - где а-сторона треугольника, которая =3, подставим в эту формулу наши данные:
S∆=(3²√3)/4=9√3/4
Таких треугольков 6 поэтому площадь основания составит:
Sосн=9√3/4×6=27√3/2
Теперь сложим эти площади и получим площадь всей поверхности пирамиды:
Sпол=27√3/2+45=13,5√3+45см²
Можно так и оставить, но если нужно вычислить полностью, то: √3≈1,73, подставим это значение:
13,5×1,73+45=23,355+45=68,355см²