Предмет: Алгебра, автор: qdwwiztbd

Найдите производную функции:

Приложения:

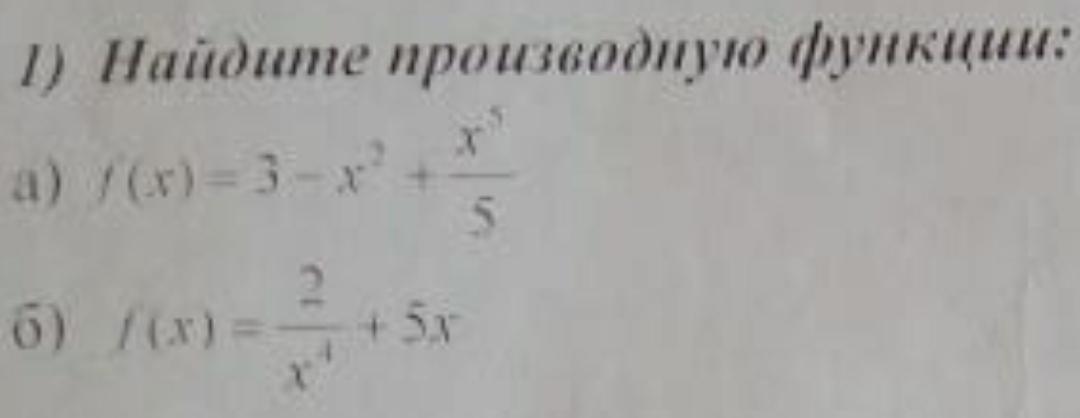
Ответы

Автор ответа: Ифигения

Ответ:

Объяснение:

Во вложении

Приложения:

Universalka: Первое задание регено неверно, так как выглядит по-другому

Ифигения: Что выглядит по-другому?)

Ифигения: А, все, заметила. Неправильно переписала условие. Сейчас поправлю.

Ифигения: Спасибо, что заметили.

qdwwiztbd: Спасибо большое!

Автор ответа: Universalka

$1)f(x)=3-x^{2} +\frac{x^{5}}{5}=3-x^{2}+\frac{1}{5}x^{5} \\\\f'(x)=3'-(x^{2})'+\frac{1}{5} *(x^{5})'=0-2x+\frac{1}{5}*5x^{4}=x^{4}-2x\\\\Otvet:\boxed{f'(x)=x^{4}-2x} \\\\\\2)f(x)=\frac{2}{x^{4}}+5x=2*x^{-4}+5x\\\\f'(x)=2*(x^{-4})'+5*x'=2*(-4x^{-5} )+5=-\frac{8}{x^{5}}+5\\\\Otvet:\boxed{f'(x)=-\frac{8}{x^{5}}+5}$