Question

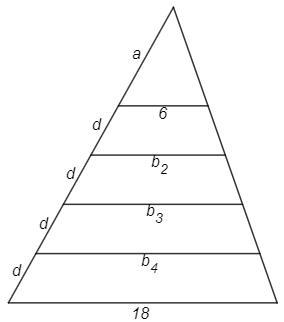
Боковая сторона трапеции разделена на четыре равные части и из точек деления проведены к другой стороне отрезки, параллельные основаниям. Найдите длины этих отрезков, если основания трапеции равны 6м и 18м.​

Answer 1

Решение:

Всего будет три отрезка. Для начала найдём среднюю из них.

Так концы этого отрезка лежать на серединах боковых сторон трапеции, то она является средней линией трапеции.

Значит её длина равна средней арифметической длин её основании.

Средний отрезок равен $\frac{6 + 18}{2}$ = 12 см

Таким же образом находим длину двух оставшихся отрезков.

Нижний отрезок равен $\frac{12 + 18}{2}$ = 15 см

Верхний отрезок равен $\frac{6 + 12}{2}$ = 9 см

Ответ: 9 см, 12 см, 15 см.

Answer 2

Продлим боковые стороны до пересечения.

Пусть сторона верхнего треугольника a, равные отрезки боковой стороны трапеции d.

Параллельные отсекают от угла подобные треугольники со сторонами a, a+d, a+2d, a+3d, a+4d.

Стороны - следовательно и основания - образуют арифметическую прогрессию.

Известны первый (6) и пятый (18) члены. Тогда шаг прогрессии (18-6)/4=3.

Прогрессия: 6, 9, 12, 15, 18 (см)