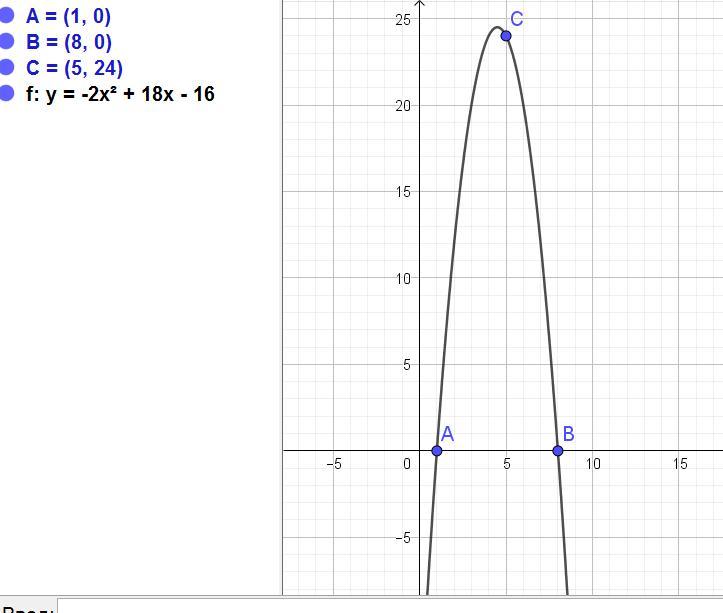
Корнями квадратного трёхчлена являются числа 1 и 8, а график проходит через точку (5, 24). Найдите свободный член этого трёхчлена
Ответы
Имеем 3 точки, принадлежащие графику функции:
А(1; 0), В(8; 0) и С(5; 24).
Составим систему их трёх уравнений, подставив в уравнение квадратного трёхчлена вида y = ax² + bx + c координаты известных точек.
a*1² + b*1 + c = 0 ,
a*8² + b*8 + c = 0,
a*5² + b*5 + c = 24.
Решение можно выполнить методом Крамера.
a b c B
25 5 1 24 Определитель 84
1 1 1 0
64 8 1 0
Заменяем 1-й столбец на вектор результатов B:
24 5 1
0 1 1 Определитель -168
0 8 1
Заменяем 2-й столбец на вектор результатов B:
25 24 1
1 0 1 Определитель 1512
64 0 1
Заменяем 3-й столбец на вектор результатов B:
25 5 24
1 1 0 Определитель -1344
64 8 0
x1= -168 / 84 = -2
x2= 1512 / 84 = 18
x3= -1344 / 84 = -16.
Ответ: свободный член этого трёхчлена равен -16.
Уравнение имеет вид у = -2х² + 18х - 16.