Предмет: Математика,
автор: tefal726
Нужно решить вот такой интеграл.
Помогите пожалуйста!
Приложения:
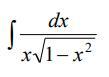
Ответы
Автор ответа:
1
Проводим замену:
Получаем:
Похожие вопросы
Предмет: Русский язык,
автор: kalimatardi
Предмет: Английский язык,
автор: spirsava67
Предмет: Қазақ тiлi,
автор: karinanet
Предмет: Математика,
автор: Аноним