Question

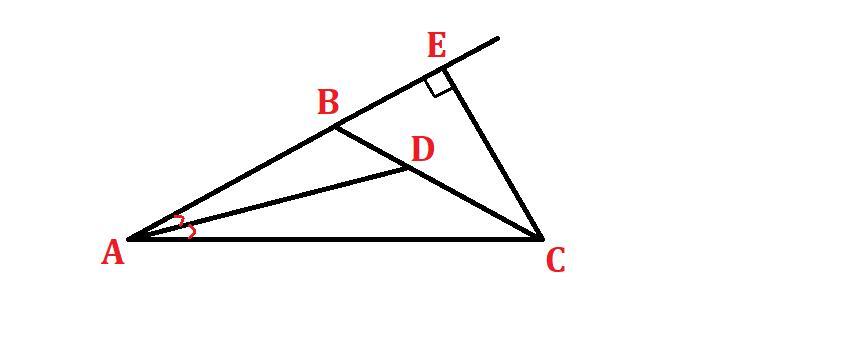
AD - биссектриса тупоугольного треугольника ABC(AB=BC). Из вершины C опущен перпендикуляр CE на сторону AB. Найти ∠ADB, если ∠ECB = 26º. !!!!!!!!!!ЭТО СРОЧНО!!!!!!!!!!!!

Answer 1

Ответ:

48°

Пошаговое объяснение:

Проведём высоту (перпендикуляр) CE на сторону AB.

Высота в тупоугольном треугольнике, проведённая из вершины острого угла, проходит во внешней области треугольника.

То есть высота CE будет вне ΔABC.

Рассмотрим ΔBEC:

∠ECB = 26°

∠BEC = 90°, т.к. CE - высота.

По свойству внешнего угла треугольника, ∠ECB + ∠BEC = ∠ABC

⇒ ∠ABC = 26° + 90° = 116°

Так как AB = BC, по условию ⇒ ΔABC - равнобедренный.

⇒ ∠BAC = ∠BCA

Сумма внутренних углов треугольника равна 180°.

⇒ ∠BAC = ∠BCA = (180° - ∠ABC) : 2 = (180° - 116°) : 2 = 64° : 2 = 32°

Так как AD - биссектриса ∠BAC ⇒ ∠BAD = ∠CAD = ∠BAC : 2 = 32° : 2 = 16°

По теореме о сумме внутренних углов треугольника ∠ADB = 180° - (∠ABC  + ∠BAD) = 180° - (116° + 16°) = 180° - 132° = 48°