Предмет: Алгебра,
автор: Аноним
Даю 50 баллов!!!! Для решения мало времени срочноо!!
Приложения:
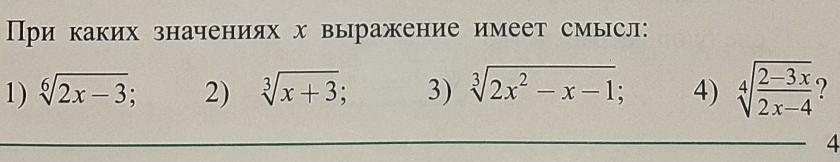
Ответы
Автор ответа:
1
Приложения:
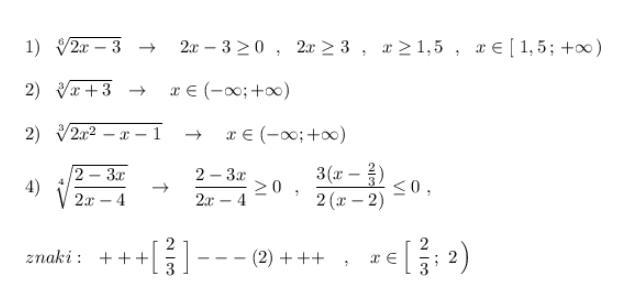
NNNLLL54:
знаки дроби считаем на указанных промежутках (метод интервалов)
Похожие вопросы
Предмет: Русский язык,
автор: iljailjalol
Предмет: Русский язык,
автор: yuliuavolkova
Предмет: Другие предметы,
автор: darinalapina1
Предмет: Математика,
автор: maliashka
Предмет: Математика,
автор: innusik2102