Предмет: Алгебра,
автор: Frog12321nik
16sin^2x-4^sinx / корень(cosx) - 1 =0
очень сроччно
Приложения:
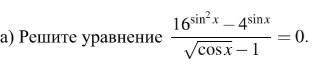
Ответы
Автор ответа:
6
Похожие вопросы
Предмет: Английский язык,
автор: mdolmatova29
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: люда2023
Предмет: Геометрия,
автор: Crysisbarca
Предмет: Химия,
автор: skogot