Предмет: Математика,
автор: yejige2779
Знайти та зобразити графічно область визначення функції. Решите плиз основы мат. анализа
Приложения:
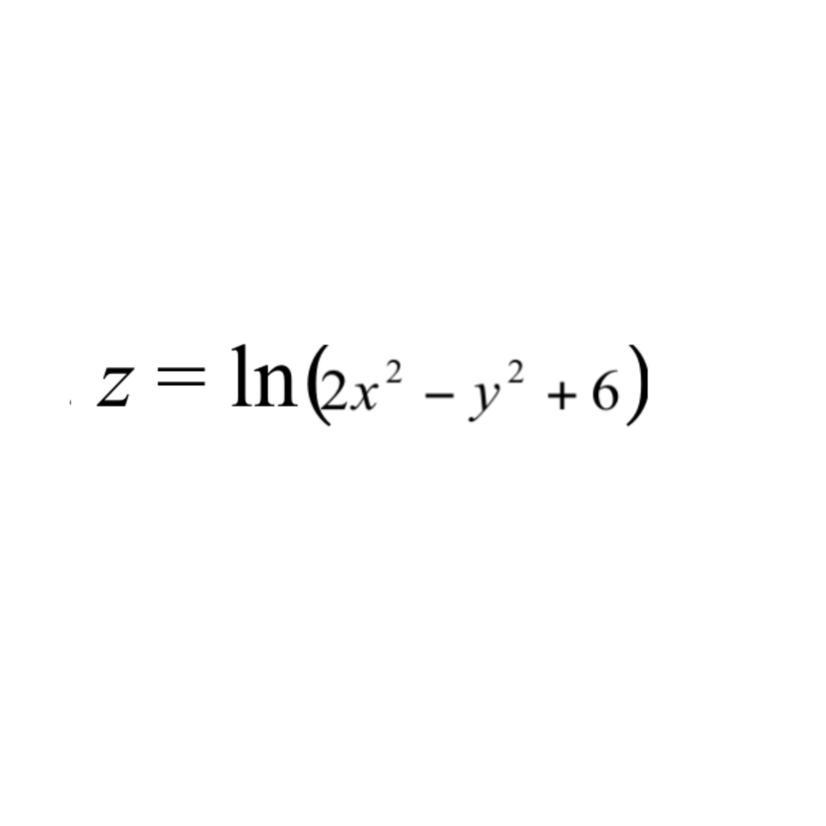
Ответы
Автор ответа:
0
Ответ:
- это гипербола ,
, центр в точке (0,0) , фокусы
и
расположены на оси ОУ в точках
и
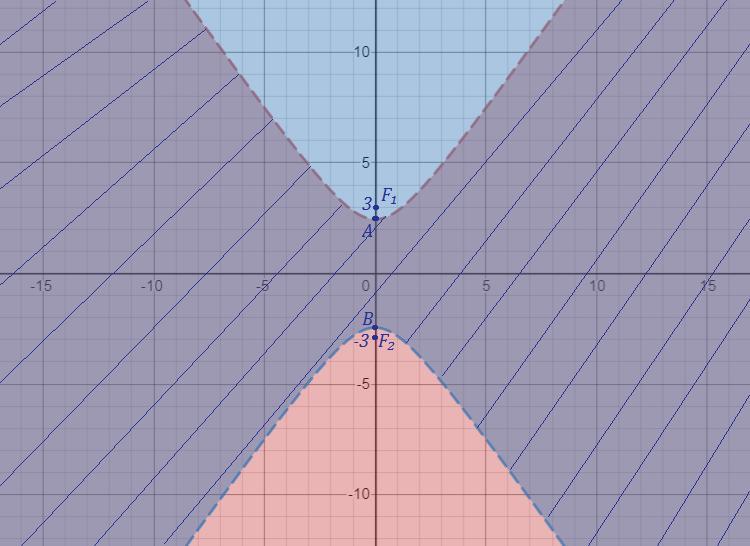
, вершины в точках A(0; 2,5) и B(0; -2,5).
Областью определения функции будет часть плоскости, лежащая между ветвями гиперболы, причём граница области, то есть сама гипербола , в ООФ не входит . На рисунке область заштрихована .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: jarik1973
Предмет: Русский язык,
автор: Moshka234
Предмет: Информатика,
автор: Propert
Предмет: Алгебра,
автор: yvrublevskiy