Предмет: Геометрия,
автор: LiNOTiK
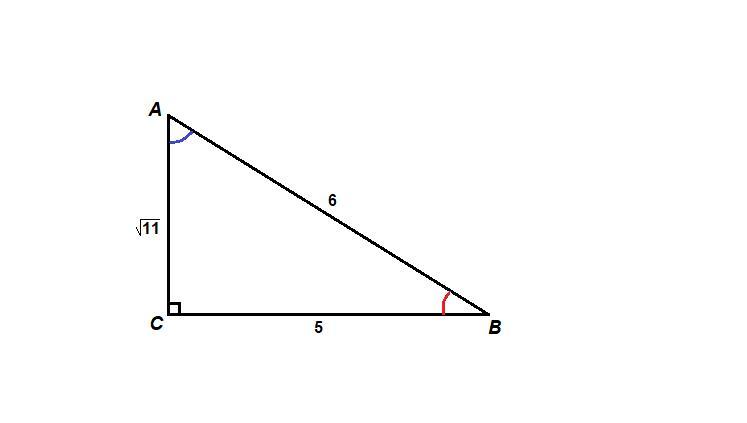
В треугольнике ABC угол C= 90°, AB= 6 см, BC= 5 см, AC= √11 см. Найдите значения синуса, косинуса, тангенса и котангенса углов A и B
Ответы
Автор ответа:
64
Ответ:
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе:
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе:
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:
Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: promokashka2003
Предмет: Українська мова,
автор: wwwouolenra85
Предмет: Русский язык,
автор: annakoz2000
Предмет: Химия,
автор: capogova
Предмет: Математика,
автор: ЛедиНуарКотБаг