Предмет: Геометрия,
автор: aruzantastanova9
Боковая сторона трапеции разделена на четыре равные части и из точек деления проведены к другой стороне отрезки параллельны основаниям Найдите длины этих отрезков если Основания трапеции равны 6 м и 18м
Ответы
Автор ответа:
4
Объяснение:
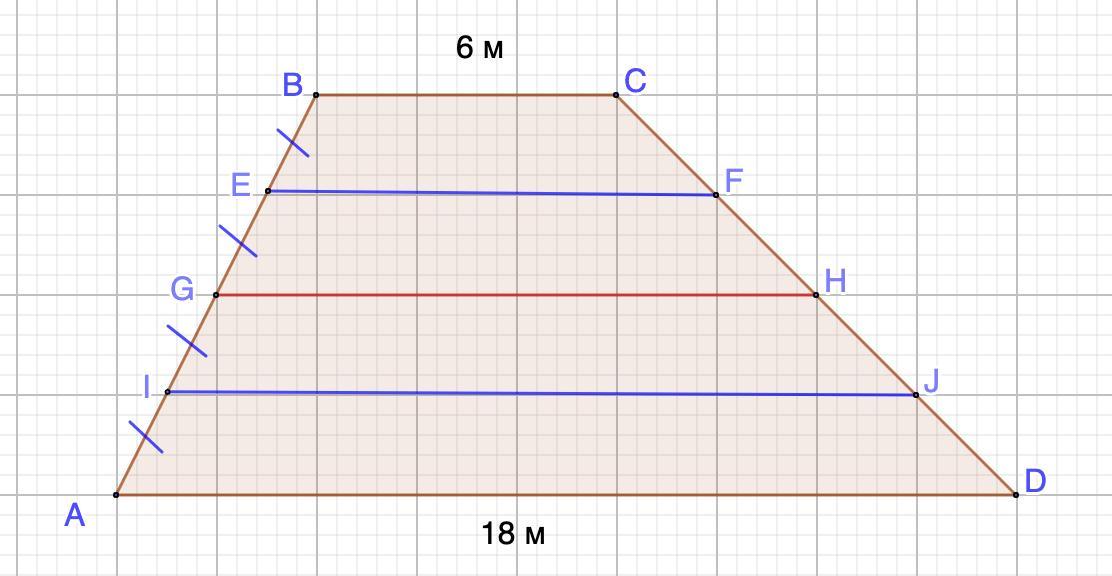
Дано: ABCD - трапеция.
AI=IG=GE=EB
EF║GH║IJ║BC║AD
BC=6 м; AD=18 м.
Найти: EF;GH;IJ.
Решение:
1) Рассмотрим ABCD.
AG=GB (условие)
GH║BC║AD (условие)
⇒ СH=HD (теорема Фалеса)
⇒GH - средняя линия.
Средняя линия трапеции равна полусумме оснований.
GH=(BC+AD):2=(6+18):2=12(м)
2) Рассмотрим GBCH - трапеция.
GE=EB (условие)
EF║GH║BC
⇒CF=FH (теорема Фалеса)
⇒ EF - средняя линия.
EF=(BC+GH):2=(6+12):2=9 (м)
3) Рассмотрим AGHD - трапеция.
AI=IG (условие)
GH║IJ║AD (условие)
⇒ IJ - средняя линия.
IJ=(GH+AD):2=(12+18):2=15 (м)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: шохиста
Предмет: Қазақ тiлi,
автор: LSDesney
Предмет: Русский язык,
автор: annushkaАнна
Предмет: Биология,
автор: Vladka2107
Предмет: Математика,
автор: анюта493